Reasoning about Knowledge
Last week, I went to Petra in Jordan together with Vasilis Syrgkanis and in the road we kept discussing about the Blue-Eyed Islanders Puzzle, posted by Terry Tao on his blog. It is a nice puzzle because it allows us to reflect on how to think about knowledge and how to make statements like “A knows that B knows that C doesn’t know fact F”. My goal in this post is not to discuss about the puzzle itself, but about a framework that allows us to think about it in a structured way. Nevertheless, I strongly recommend the puzzle, first because it is a lot of fun, and second, because it gives a great non-trivial example to think about this kind of thing. But first, a photo from Petra:
And then some references:
- Classic: “Agreeing to Disagree” (Robert Aumann)
- Survey:Â “Common Knowledge” (John Geanakoplos)
- Book: “Reasoning about Knowledge” (Fagin, Halpern, Moses, Vardi)
I first read Aumann’s classic, which is a very beautiful and short paper — but where I got most intuition (and fun) was reading Chapter 2 of Reasoning About Knowledge. So, I’ll show here something in between of what Chapter 2 presents and what Geanakoplos’ survey presents (which is also an amazing source).
We want to reason about the world and the first thing we need is a set representing all possible states the world can take. Each
is called a state of the world and completely described the world we are trying to reason about. To illustrate the example, consider the situation where there are
people in a room and each person has a number
in his head. Person
can see the number of everyone else, except his. We want to reason about this situation, so a good way to describe the world is to simply define
of all
-strings. We define an event to be simply a subset of the possible states of the world, i.e., some set
. For example, the even that player
has number
in his head is simply:
. We could also think about the event
that the sum of the numbers is odd, which would be:
. Now, we need to define what it means for some person to know some event.
For each person , his knowledge structure is defined by a partition
ofÂ
. The rough intuition is that player
is unable to distinguish two elements
in the same cell of partition
. For each
,
is the cell of partition
containing
. The way I see knowledge representation is that if
is the true state of the world, then person
knows that the true state of the world is some element in
.
Definition: We say that person
knows event
on the state of the world
is
. Therefore, if person
knows event
, the world must be in some state
.
Above we define the knowledge operator . Below, there is a picture in which we represent its action:
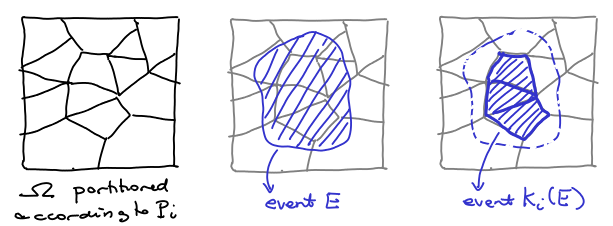 Now, this allows us to represent the fact that person
Now, this allows us to represent the fact that person knows that person
knows of event
as the event
. Now, the fact the person
knows that person
doesn’t know that person
knows event
can be represented as:
, where
.
An equivalent and axiomatic way of defining the knowledge operator is by defining it as an operator such that:
Notice that axioms 1-4 define exactly a topology and together with 5 it is a topology that is closed under complement. The last two properties are more interesting: they say that if player knows something, then he knows that he knows and if the doesn’t know something, he knows that he doesn’t know. Aumann goes ahead and defines the notion of common knowledge:
Definition: We say that an event
is common knowledge at
if for any
and for any sequence
where
are players, then
.
Suppose that is a partition that is a simultaneous coarsening of
, then for all cells
of this partition, either
or
is common knowledge.
An alternative representation is to represent $\Omega$ as nodes in a graph and add an edge between and
labeled with
if they are in the same cell of
. Now, given the true state of the world
, one can easily calculate the smallest event
such that
knows
: this is exactly the states that are reached from
just following edges labeled with
, which is easily recognizable as
.
Now, what is the smallest set that knows that
knows ? Those are the elements that we can arrive from a path following first an edge labeled
and then an edge labeled
. Extending this reasoning, it is easy to see that the smallest set that is common knowledge at
are all the elements reachable from some path in this graph.
More about knowledge representation and reasoning about knowledge in future posts. In any case, I can’t recommend enough the references above.

