Archive

Posts Tagged ‘logic’

Reasoning about Knowledge

April 16th, 2011 No comments

Last week, I went to Petra in Jordan together with Vasilis Syrgkanis and in the road we kept discussing about the Blue-Eyed Islanders Puzzle, posted by Terry Tao on his blog. It is a nice puzzle because it allows us to reflect on how to think about knowledge and how to make statements like “A knows that B knows that C doesn’t know fact F”. My goal in this post is not to discuss about the puzzle itself, but about a framework that allows us to think about it in a structured way. Nevertheless, I strongly recommend the puzzle, first because it is a lot of fun, and second, because it gives a great non-trivial example to think about this kind of thing. But first, a photo from Petra:

And then some references:

I first read Aumann’s classic, which is a very beautiful and short paper — but where I got most intuition (and fun) was reading Chapter 2 of Reasoning About Knowledge.  So, I’ll show here something in between of what Chapter 2 presents and what Geanakoplos’ survey presents (which is also an amazing source).

We want to reason about the world and the first thing we need is a set \Omega representing all possible states the world can take. Each \omega \in \Omega is called a state of the world and completely described the world we are trying to reason about. To illustrate the example, consider the situation where there are n people in a room and each person has a number x_i \in \{0,1\} in his head. Person i can see the number of everyone else, except his. We want to reason about this situation, so a good way to describe the world is to simply define \Omega = \{0,1\}^n of all 0,1-strings. We define an event to be simply a subset of the possible states of the world, i.e., some set E \subseteq \Omega. For example, the even that player 1 has number 0 in his head is simply: E = \{ x \in \Omega; x_1 = 0 \}. We could also think about the event E' that the sum of the numbers is odd, which would be: E' = \{ x \in \Omega; \sum_i x_i \text{ mod } 2 = 1 \}. Now, we need to define what it means for some person to know some event.

For each person i, his knowledge structure is defined by a partition P_i of  \Omega. The rough intuition is that player i is unable to distinguish two elements \omega_1, \omega_2 in the same cell of partition P_i. For each \omega, P_i(\omega) is the cell of partition P_i containing \omega . The way I see knowledge representation is that if \omega is the true state of the world, then person i knows that the true state of the world is some element in P_i(\omega).

Definition: We say that person i knows event E on the state of the world \omega is P_i(\omega) \subseteq E. Therefore, if person i knows event E, the world must be in some state K_i(E) := \{\omega \in \Omega; P_i(\omega) \subseteq E\}.

Above we define the knowledge operator K_i(\cdot). Below, there is a picture in which we represent its action:

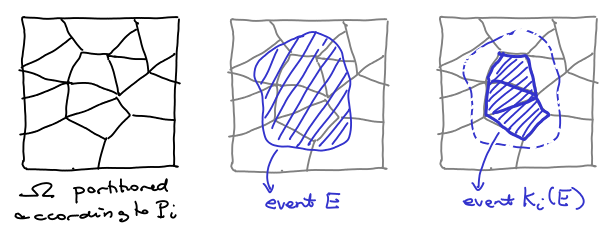Now, this allows us to represent the fact that person 1 knows that person 2 knows of event E as the event K_1(K_2(E)). Now, the fact the person 1 knows that person 2 doesn’t know that person 1 knows event E can be represented as: K_1(\neg K_2(K_1(E))), where \neg E := \Omega \setminus E.

An equivalent and axiomatic way of defining the knowledge operator is by defining it as an operator K_i: 2^\Omega \rightarrow 2^\Omega such that:

  1. K_i(\Omega) = \Omega
  2. K_i(A) \cap K_i(B) = K_i(A \cap B)
  3. K_i(A) \subseteq A
  4. K_i(K_i(A)) = K_i(A)
  5. \neg K_i(A) = K_i(\neg K_i(A))

Notice that axioms 1-4 define exactly a topology and together with 5 it is a topology that is closed under complement. The last two properties are more interesting: they say that if player i knows something, then he knows that he knows and if the doesn’t know something, he knows that he doesn’t know. Aumann goes ahead and defines the notion of common knowledge:

Definition: We say that an event E is common knowledge at \omega if for any k and for any sequence i(1), \hdots, i(k) where i(j) are players, then \omega \in K_{i(1)} K_{i(2)} \hdots K_{i(k)} E.

Suppose that P' is a partition that is a simultaneous coarsening of P_1, \hdots, P_k, then for all cells C of this partition, either C or \neg C is common knowledge.

An alternative representation is to represent $\Omega$ as nodes in a graph and add an edge between \omega_1 and \omega_2 labeled with i if they are in the same cell of P_i. Now, given the true state of the world \omega \in \Omega, one can easily calculate the smallest event E such that i knows E: this is exactly the states that are reached from \omega just following edges labeled with i, which is easily recognizable as P_i(\omega).

Now, what is the smallest set that 1 knows that 2 knows ? Those are the elements that we can arrive from a path following first an edge labeled 1 and then an edge labeled 2. Extending this reasoning, it is easy to see that the smallest set that is common knowledge at \omega are all the elements reachable from some path in this graph.

More about knowledge representation and reasoning about knowledge in future posts. In any case, I can’t recommend enough the references above.

Categories: theory Tags: ,

Prisioners and boxes

July 13th, 2009 No comments

In EC, Sean, one of my friends from UBC, told me an interesting puzzle. I liked both the problem and the solution a lot and since the solution has a lot of interesting ideas, I felt like writing about it. EC also reminded me that puzzles are fun and that I should use a bit more of my time solving those nice math problems. The problem is like that:

There were 100 prisoners and 3 different rooms, say A, B and C. In the beginning they are all in room A. In room B there are 100 boxes, each one containing the name of a different prisoner. One at a time, the prisoners are brought from A to B and in B they can open 50 boxes. Then they are brought to room C. (They cannot change the state of room B, so it is the same of having 100 identical copies of room B and bringing each prisoner to one of the rooms. They cannot leave signals in the room). If each prisoner finds his owns name, they are all freed. They only think they can do is to agree on a certain strategy while they are all in room A and then follow that strategy. If they don’t succeed, the names are randomly rearranged and they can try again the next day. Find a strategy for them so that they succeed in less than one week (in expectation).

A few things I need to drawn your attention to: (i) it is purely a math puzzle, there are no word-games. If something is obscure, it was my fault and it was not intentional, (ii) the fact that names were rearranged in boxes randomly is very important. The solution doesn’t work if the distribution is adversarial. (iii) if each of them pick 50 boxes at random, than each prisioner has 1/2 probability of succeeding, so they take 2^{100} days in expectation, what is a lot. How to reduce it to about seven days?

Structure of random permutations

The solution has to do with the structure of a permutation drawn at random. Consider one of the n! permutation is sampled uniform at random. We can write each permutation as a product of disjoint cycles. For example, the permutation \sigma = \begin{pmatrix} 1&2&3&4&5&6\\4&5&6&3&2&1 \end{pmatrix} can be written as a product of two disjoint cycles: \sigma = ( 1,4,3,6 ) (2,5). In the language of boxes and prisoners, it is: box a_1 contains the name of prisoner a_2, then box a_2 contains the name of prisoner a_3 and so on, until box a_k contains name of prisoner a_1. This is the cycle (a_1, a_2, \hdots, a_k). If  all the cycles have length smaller than n/2 where n is the number of prisoners, then there is a simple strategy: we can consider that each prisoner corresponds to one box a priori (say prisoners have number 1, \hdots, n and boxes also have numbers 1, \hdots, n. The permutation  is define by the function \sigma from the box number to the number of the prisoner whose name is inside the box. Now, prisoner k opens box k, reads the name of the prisoner inside the box and the box with that number, then he looks at the number of the prisoner inside that other box and continues following the cycle.

The probability of success is the same of the probability that a permutation \pi drawn at random has no cycle of size greater than n/2. Let $\phi_p$ be the probability that a random permutation has a cycle of length p, where p > n/2. This is a simple exercise of combinatorics: we can have \begin{pmatrix} n \\ p \end{pmatrix} ways of picking the p elements that will form the p-cycle. There are (n-p)! permutations for the remaining n-p elements and (p-1)! cycles that can be formed with those p elements. So, we have:

\displaystyle \phi_p = \frac{1}{n!} \begin{pmatrix} n \\ p \end{pmatrix} (n-p)! (p-1)! = \frac{1}{p}

And therefore the probability of having a cycle with length more than n/2 is \sum_{p=1+n/2}^n \frac{1}{p}. For n = 100, we get about 0.68, therefore the expected time before one permutation with no cycle larger than n/2 appears is \frac{1}{1-0.68} \approx 3.3 days. Much less than one week, actually!

Structure and Randomness

The solution to this puzzle explores the structure in randomness. A lot of work in computer science is based on looking at the structure (or expected structure) of a randomly chosen object. A very elegant kind of proof consists in creating a random process that generates object and prove that some object exists because is happens with positive probability. One simple, yet very beautiful example, is the following theorem: given any logic expression in 3-CNF form, i.e., one expression of the kind:

\displaystyle \bigwedge_i (a_{i1} \vee a_{i2} \vee a_{i3})

where a_{ij} \in \{ x_i, \tilde x_i\}, there is an assignment of x_i to \{0,1\} that satisfies 7/8 of the clauses. Even though the statement of this result has no probability in it, the proof is probabilitic. Consider a random assignment to the variables. Then each clause is satisfied with probability 7/8. Because of linearity of expectation, the expected number of satisfied clauses is 7/8 of the total. Since this is the expected number of satisfied clauses, there must be at least one assignments satisfying more than 7/8.

This kind of proof is called the probabilistic method. There are also a lot of other cool things exploring randomness in computer science, in design of algorithms, criptography, complexity theory, … Recently I read a nice blog post by Lipton, he discusses ways he would try to solve the P vs NP problem. One comment I found really interesting and exciting (but that I don’t quite understand yet) is that we could, maybe, separate the SAT-3 instances in “random” and “structured” instances and try to use different methods exploring randomness or structure in each of them.

\left(\begin{array}{ccc}1&2&3\\3&2&1\end{array}\ri  ght)

Categories: puzzles Tags: , ,