Three interesting puzzles
Here are three puzzles I got from 3 different people recently. The first I got from Charles, who got it from a problem set of the Brazilian Programming Competition.
Puzzle #1: Given
and a vector of in-degrees and out-degrees
and
for
, find if there is a simple directed graph on
nodes with those in and out-degrees in time
. By a simple directed graph, I mean at most one edge between each pair
, allowing self loops
.
Solving this problem in time is easy using a max-flow computation – simply consider a bipartite graph with and edge
between each pair with capacity
. Add a source and connect to each node in the left size with capacity
and add also a sink in the natural way, compute max-flow and check if it is
. But it turns out we can do it in a lot more efficient way. The solution I thought works in time
but maybe there is a linear solution out there. If you know of one, I am curious.
The second puzzle was given to me by Hyung-Chan An:
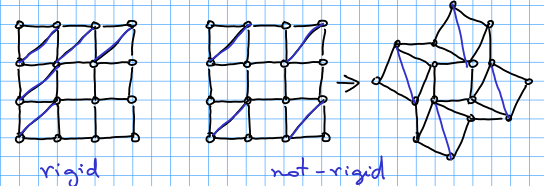
Puzzle #2: There is grid of size
formed by rigid bars. Some cells of the grid have a rigid bar in the diagonal, making that whole square rigid. The question is to decide, given a grid and the location of the diagonal bars if the entire structure is rigid or not. By rigid I mean, being able to be deformed.
We thought right away in a linear algebraic formulation: look at each node and create a variable for each of the 4 angles around it. Now, write linear equations saying that some variables sum to 360, since they are around one node. Equations saying that some variable must be 90 (because it is in a rigid cell). Now, for the variables internal to each square, write that opposite angles must be equal (since all the edges are of equal length) and then you have a linear system of type where
are the variables (angles). Now, we need to check if this system admits more then one solution. We know a trivial solution to it, which is all variable is 90. So, we just need to check if the matrix
has full rank.
It turns out this problem has a much more beautiful and elegant solution and it is totally combinatorial – it is based on verifying that a certain bipartite graph is connected. You can read more about this solution in Bracing rectangular frameworks. I by (Bolker and Crapo 1979). A cute idea is to use the the following more general linear system (which works for rigidity in any number of dimensions). Consider a rigid bar from point to point
. If the structure is not rigid, then there is a movement it can make: let
and
be the instantaneous velocities of points
and
. If
are the movements of points
, then it must hold that:
, so taking derivatives we have:
This is a linear system in the velocities. Now, our job is to check if there are non zero velocities, which again is to check that the matrix of the linear system is or is not full-rank. Â An interesting thing is that if we look at this question for the grid above, this matrix will be the matrix of a combinatorial problem! So we can simply check if it has full rank by solving the combinatorial problem. Look at the paper for more details.
The third puzzle I found in the amazing website called The Puzzle Toad, which is CMU’s puzzle website:
Puzzle #3: There is a game played between Arthur and Merlin. There is a table with
lamps disposed in a circle, initially some are on and some are off. In each timestep, Arthur writes down the position of the lamps that are off. Then Merlin (in an adversarial way) rotates the table. The Arthur’s servant goes and flips (on –> off, off –> on) the lamps whose position Arthur wrote down (notice now he won’t be flipping the correct lamps, since Merlin rotated the table. if Arthur wrote lamp 1 and Merlin rotated the table by 3 positions, the servant will actually be flipping lamp 4. The question is: given
and an initial position of the table, is there a strategy for Merlin  such that Arthur never manages to turn all the lamps on.
See here for a better description and a link to the solution. For no matter what Merlin does, Arthur always manages to turn on all the lamps eventually, where eventually means in
time. The solution is a very pretty (and simple) algebraic argument. I found this problem really nice.