Bimatrix games
This week in Israel is the Workshop on Innovations in Algorithmic Game Theory, which has been a collection of amazing talks and I thought of blogging about something new I learned here. First, Paul Goldberg gave an amazing talk about the Lemke-Howson algorithm and Homotopy Methods. Later, during the poster session Jugal Garg presented the impressive work on an exact algorithm for finding Nash equilibria in rank 1 bimatrix games. Both have in common the use of homotopy, which I found I quite cool idea – and has been present in Game Theory for a while, but I didn’t know about. They also have to do with improving the understanding we have on the Lemke-Howson Algorithm – a (potentially exponential time) algorithm to find Nash equilibrium in 2-person bi-matrix games, but that seems to work pretty well in practice. As always, I though that blogging about it would be a good idea in order to understand those concepts well.
Bimatrix Game and How to compute equilibrium
Bimatrix game is the simplest class of games studied. Basically it is a player game, with
strategies for player
and
strategies for player 2 which is represented by a pair of
matrices
. Let
represent a probability distribution that player
assigns to his strategies and
be the same for player
. This way, the players experience utilities:
The best understood class of those games is the one where , called zero-sum games. For this class, computing a Nash equilibrium is very easy and it is given by the famous min-max theorem: player
finds
maximizing
where
is the
-th unit vector. Similarly player
finds
maximizing
. Then the pair of strategies obtained is a Nash equilibrium – and this verifying that is not hard.
When , the problems gets a lot more complicated. Proving that equilibrium exist can be done using various fixed point theorems, as Brouwer or Kakutani. There is a very simple exponential time algorithm for finding it and the key observation is the following, if
is a Nash equilibrium then:
which means that each strategy for player is either in the support or is a best response. Proving that is trivial (if some strategy is in the support and is not a best response, then reducing the probability we play it is an improving deviation). Therefore if we just guess the support of
and the support of
we just need to find some strategies with this support satisfying the inequalities above. This can be done using a simple LP. This is clearly not very efficient, since it involves solving
LPs. A still exponential, but a lot more practical method, is:
Lemke-Howson Algorithm
A good overview of the L-H algorithm can be found in those lecture notes or in a more detailed version in third chapter of the AGT book (a pdf can be found in Tim’s website). Here I’ll present a quick overview. The main idea is to define the best-response polytopes and
:
The intuition is that a point represents the fact that the payoff
of player
when player
plays
is at least
. We could re-write as
.
Each of the polytopes has inequalities and
equality. Given
we define
as the indices of the tight inequalities in
and similarly we define
as the indices of the tight inequalities in
. The theorem in the previous section can be rephrased as:
is Nash equilibrium iff
So we need to look at points in the polytope below that are fully-labeled. And the way that this is done in L-H is quite ingenious – it is a similar idea that is used by the Simplex Method – walking through the vertices of the polytope looking for the desired vertex. In order to do it, let’s define another polytope:
Note that there is a clear bijection between and
. This is a projective transformation given by
. Notice that the labels are preserved by this transformation and the vertex and edges of the polytope are mapped almost 1-1 (except the vertex
). Notice a couple of details:
1. A vertex in corresponds to a point with
labels. A vertex in
corresponds to a point with
labels.
2. The point corresponds to a fully-labeled point of
, unfortunately this is the only fully-labeled point that doesn’t correspond to a Nash equilibrium.
3. By taking an edge of the polytope (which is define by labels in
and
labels in
. We can move between two nodes that are almost fully labeled.
The idea is to consider the set of nodes that are almost fully-labeled: fix some label and consider all the nodes such that
. Those points are either
, a Nash equilibrium or they have one duplicated label, since
. An edge is composed of
labels (no duplicated labels). So, one almost fully-labeled point that is not a Nash or
is only connected to two other vertices via an edge (which correspond to dropping one of the duplicated labels and following the corresponding edge).
This gives us a topology of the space of Nash equilibria. This tells us a couple of facts: (1) we can find a Nash equilibrium by starting in and following the L-H path. In the end of the path, we must find a Nash equilibrium. (ii) If the polytope is not degenerate, then there is an odd number of Nash equilibria and they are connected by L-H edges in the following way:
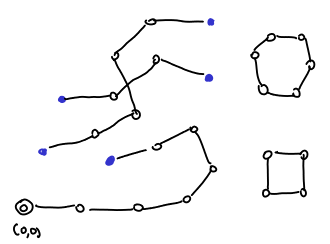 where the blue dots are the Nash equilibria, the white dots are the almost fully-labeled points and the edges are the L-H edges. The number of Nash equilibria are odd by a simple parity argument.
where the blue dots are the Nash equilibria, the white dots are the almost fully-labeled points and the edges are the L-H edges. The number of Nash equilibria are odd by a simple parity argument.
The classic way in which simplex-like methods walk through the vertices of a polytope is by pivoting. The same way we can implement Lemke-Howson. For an explanation on the implementation, please look at the chapter 3 of the AGT book.
One can ask if we could modify the L-H path following to go through the path faster. Recently, Goldberg, Papadimitriou and Savani proved that finding the Nash equilibrium that L-H outputs is PSPACE-complete. So, in principle, finding this specific equilibrium, seems harder than finding any Nash, which is PPAD-complete.
My current plan is on some other blog posts on Bimatrix games. I wanted to discuss two things: first the homotopy methods and homotopy fixed-point-theorems (which is the heart of the two papers mentioned above) and about new techniques for solving zero-matrix where the strategy space is exponential.