Currently I’ve been trying to understand more about the dynamics of markets and basic concepts of microeconomic theory and, as always, writing a blog post will help me to keep my ideas clear. First, why are markets interesting from a computer scientist/mathematician point of view?
- Markets are multi-objective optimization problems: one can think of the possible state of a market some point in a space of possible
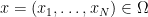 . Each player of the market controls one variable, say
. Each player of the market controls one variable, say  and is interested in maximizing one objective function
and is interested in maximizing one objective function  . So, player
. So, player  is trying to set
is trying to set 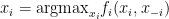 .
.
- Markets are a computational model: one can think of a market as a way of performing a certain computation – as extracting some kind of information, as a prediction market, stock exchanges, … If we think of it as a computational device, we are asking the same questions: given those preferences which are implicit functions to each of the agents, calculate “fair” prices of items.
- Markets are distributed systems where each part of the system has a selfish interest.
A market is composed by a set 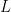 of commodities,
of commodities,  of consumers and
of consumers and  of producers. Now, we describe how to characterize each of them:
of producers. Now, we describe how to characterize each of them:
- Each consumer is defined by a set
 of commodities combinations he is interested (typically we take
of commodities combinations he is interested (typically we take 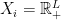 ) and an utility function
) and an utility function  expressing his interest for this bundle of commodities. Consumer
expressing his interest for this bundle of commodities. Consumer  will try to maximize
will try to maximize 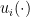 in a further restricted
in a further restricted 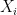 .
.
- Each producer is define by a set
 it has the capacity to produce.
it has the capacity to produce.
- Endowments: Each consumer comes to the market with an initial endowment
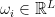 , so for
, so for  ,
, 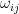 is the amount of commodity
is the amount of commodity  that consumer
that consumer  originally has. The initial total endowment of the market is given by
originally has. The initial total endowment of the market is given by 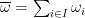 , which is a vector indicating how much of each commodity originally exists in the market.
, which is a vector indicating how much of each commodity originally exists in the market.
- Shares: consumers have shares in the companies, so for
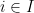 ,
,  , consumer
, consumer  has
has  shares of company
shares of company  , such that
, such that 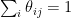 .
.
Something very crucial is missing in this picture: a way to compare commodities and something that makes exchanges possible: the answer to that is to attribute prices to the items. How to attribute prices to the items so that the market works fine? A price vector is a vector  . Consider the following scenario after prices
. Consider the following scenario after prices  are established to commodities:
are established to commodities:
- by producing
 , company
, company  gets profit
gets profit  , so each company will try to maximize its profit producing
, so each company will try to maximize its profit producing  .
.
- each consumer sells its initial endowment and gets the profit respective to the companies he owns. So, consumer
 gets
gets  .
.
- now consumer
 uses the money he has to buy the best bundle he can afford, which is
uses the money he has to buy the best bundle he can afford, which is 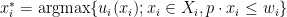 .
.
The amount of commodities in the market must conserve, so that is possible only if we get:
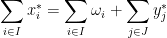
First, it is not clear if such a price vector exists. If it exists, is it unique? If this is an equilibrium, is it the best thing for the consumers? How those prices can be set in practice without a centralized authority? Can people lie? Below, let’s collect a couple of questions I’ll try to answer (yes, no or unknown) in this and the following posts.
Question 1: Does a price vector  always exist that generates an equilibrium?
always exist that generates an equilibrium?
Question 2: If it exists, is it unique?
Question 3: Can we describe an efficent method to find 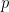 ?
?
Question 4: Is it the best thing for the consumers in the following sense: if 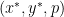 is an equilibrium, are there feasible
is an equilibrium, are there feasible  such that
such that 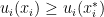 and for at least one consumer
and for at least one consumer 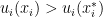 ? (This is called Pareto improvement)
? (This is called Pareto improvement)
Question 5: A central authority could use the knowledge about functions 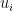 and endowments
and endowments 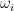 to calculate the price vector
to calculate the price vector 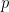 using some method. Can consumers
using some method. Can consumers  be better off by lieing about their utility and endowments?
be better off by lieing about their utility and endowments?
Question 6: How prices get defined without a central authority? Is there a dynamic/game-theoretical model to that?
For simplicity, let’s think of Exchange Economies, which are economies with no producers. Let’s define it formally:
Definition 1 An exchange economy is composed by a set of commodities 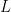 and a set of consumers
and a set of consumers  each with an utility
each with an utility  and an initial endowment
and an initial endowment 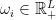 .
.
Definition 2 A price vector  is a Walrasian equilibrium for an exchange economy
is a Walrasian equilibrium for an exchange economy 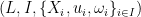 if there is
if there is 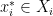 such that:
such that:
-
 s.t.
s.t. 
-
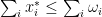
-
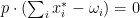
The first condition says that each consumer is maximizing his utility given his prices, the second says that we can’t buy more commodities than what is available in the market and the third, called Walras’ Law, says that if there is surplus of a certain product, it should have price zero. It is by far the most unnatural of those, but it can be easily justifiable in some circumnstances: suppose we say that utilities are non-satiated if for each  and
and  , there is
, there is 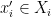 ,
,  such that
such that  . If
. If 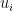 are differentiable, that would mean
are differentiable, that would mean 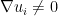 , for example a linear function
, for example a linear function  with some
with some 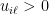 . In that case,
. In that case, 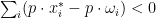 and some player has money surplus and therefore he could increase his utility.
and some player has money surplus and therefore he could increase his utility.
Now, we define for each price vector 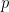 the excess demand function
the excess demand function  and
and  . Now, under non-satiated utilities, by the last argument, we have that
. Now, under non-satiated utilities, by the last argument, we have that 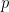 is an equilibrium vector iff
is an equilibrium vector iff 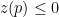 . Actually, if
. Actually, if 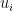 are also strong monotone, i.e.,
are also strong monotone, i.e.,  for each
for each  , then it becomes:
, then it becomes: 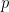 is an equilibrium iff
is an equilibrium iff 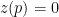 , which means that the market clears:
, which means that the market clears:

The question that is easier to answer is Question 4 and it is sometimes refered as the First Fundamental Theorem of Welfare Economics:
Theorem 3 Given non-satiated preferences, each equilibrium  is Pareto, i.e. there is no other feasible allocation
is Pareto, i.e. there is no other feasible allocation  such that for all
such that for all  ,
, 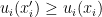 with the inequality strict for at least one component.
with the inequality strict for at least one component.
Proof: Suppose there were, since 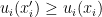 then
then 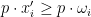 , because if
, because if  then we could improve the utility of
then we could improve the utility of  still within the budget, contradicting the optimality of
still within the budget, contradicting the optimality of  for that budget. And clearly
for that budget. And clearly  implies
implies 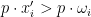 .
.
Summing over  , we get
, we get  , what is a contradiction, because since
, what is a contradiction, because since  is feasible,
is feasible,  and therefore
and therefore  .
. 
Now, let’s tackle Question 1. We assume linearly of utility: 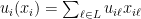 for
for 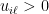 . This gives us strong monotonicity and local nonsatiated preferences.
. This gives us strong monotonicity and local nonsatiated preferences.
Theorem 4 Under linear utilities, there is always an equilibrium price vector 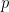 .
.
Consider the function  defined above:
defined above:  where
where  is the bundle of best possible utility. Now, since we are using linear utilities we can’t guarantee there will be only one such bundle, so instead of considering a function, consider
is the bundle of best possible utility. Now, since we are using linear utilities we can’t guarantee there will be only one such bundle, so instead of considering a function, consider  and
and  as being correspondences:
as being correspondences:  , i.e.,
, i.e., 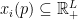 is the set of all allocations that maximize
is the set of all allocations that maximize  subject to
subject to 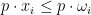 . Since
. Since 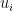 are linear functionals, we can calculate
are linear functionals, we can calculate  by a Fractional Knapsack algorithm: we sort commodities
by a Fractional Knapsack algorithm: we sort commodities  by
by  and start buying in the cost-benefit order (the ones that provide more utility per buck spent). Most of the time there will be just one solution, but in points where
and start buying in the cost-benefit order (the ones that provide more utility per buck spent). Most of the time there will be just one solution, but in points where  , then
, then  might be a convex region. This correpondence is upper hemicontinuous, which is the correspondence analogue to continuity for functions. As Wikipedia defines:
might be a convex region. This correpondence is upper hemicontinuous, which is the correspondence analogue to continuity for functions. As Wikipedia defines:
Definition 5 A correspondence 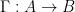 is said to be upper hemicontinuous at the point
is said to be upper hemicontinuous at the point  if for any open neighbourhood
if for any open neighbourhood 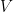 of
of  there exists a neighbourhood
there exists a neighbourhood  of a such that
of a such that  is a subset of
is a subset of 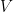 for all
for all  in
in  .
.
It is not hard to see that  is upper hemicontinuous according to that definition. Our goal is to prove that there is one price vector
is upper hemicontinuous according to that definition. Our goal is to prove that there is one price vector 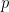 for which
for which  or:
or:  . To prove that we use Kakutani’s Fixed Point Theorem. Before we go into that, we’ll explore some other properties of
. To prove that we use Kakutani’s Fixed Point Theorem. Before we go into that, we’ll explore some other properties of  :
:
- 0-Homogeneous:
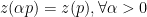
- Walras’ Law:
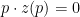 . For any
. For any 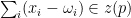 we know
we know  by the definition of
by the definition of  . So, if it not zero, some
. So, if it not zero, some  has money surplus what is absurd given that preferences are strongly monotone.
has money surplus what is absurd given that preferences are strongly monotone.
- Bounded:
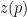 is bounded from below, i.e.,
is bounded from below, i.e., 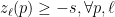 for some
for some  . Simply take
. Simply take 
- Boundary behavior: if
 with
with  , then
, then 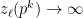 . That is clear from the fractional knapsack algorithm when one desirable item gets price zero.
. That is clear from the fractional knapsack algorithm when one desirable item gets price zero.
Now, we are in shape for applying Kakutani’s Fixed Point Theorem:
Theorem 6 (Kakutani, 1941) If  is an upper hemicontinuous correspondence such that
is an upper hemicontinuous correspondence such that 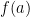 is a convex non-empty set for all
is a convex non-empty set for all  then
then 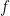 has a fixed point, i.e.,
has a fixed point, i.e., 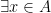 s.t.
s.t. 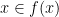 .
.
Since prices are 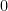 -homogeneous, consider the simplex
-homogeneous, consider the simplex  , its relative interior
, its relative interior 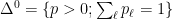 and the boundary
and the boundary 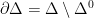 . Now we define the following price correcting correspondence
. Now we define the following price correcting correspondence 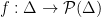 .
.
If some price  is set, it generates demand
is set, it generates demand  . For that demand, the price that would maximize profit would be
. For that demand, the price that would maximize profit would be 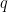 , i.e.
, i.e. 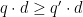 for all
for all  . It is natural to re-adjust the prices to
. It is natural to re-adjust the prices to 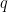 . So we define for
. So we define for  :
:
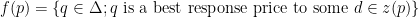
and for 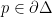 :
:
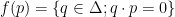
Now, I claim that this correspondence satisfies the conditions in Kakutani’s Theorem. We skip a formal proof of this fact, but this is intuitive for the interior 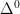 – let’s give the intuition why this is true as we approach the boundary: if
– let’s give the intuition why this is true as we approach the boundary: if  , then
, then 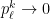 , therefore the demans explodes:
, therefore the demans explodes: 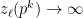 and as a result the best thing to do is to set the prices of those commodities much higher than the rest. Therefore, the price of the commodities whose demand explode are positive while the prices of the commodities where the price doesn’t get value zero.
and as a result the best thing to do is to set the prices of those commodities much higher than the rest. Therefore, the price of the commodities whose demand explode are positive while the prices of the commodities where the price doesn’t get value zero.
Now, after waiving our hands about the upper continuity of 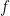 , we have by Kakutani’s Theorem a point
, we have by Kakutani’s Theorem a point 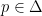 such that
such that 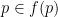 . By the definition of
. By the definition of 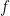 we must have
we must have  (because for
(because for 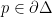 ,
,  . Now, I claim
. Now, I claim 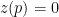 . In fact if
. In fact if  , still
, still 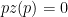 by Walras’ Law. So, if
by Walras’ Law. So, if  then there is
then there is  with
with 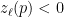 and therefore
and therefore 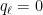 for all
for all 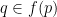 , and
, and  . For this reason
. For this reason 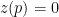 .
.
In the next blog post (or serie of blog posts, let’s see) we discuss issues related to the other questions: uniqueness, dynamics, game-theoretical considerations, …
people in a line, and each has a
number on his hat. Each player can look to the numbers of the players in front of him. So, if
is the number of player
, then player
knows
. Now, from
the players will say his own number. Is there a protocol such that players
will get their own number right? (Notice that they hear what the players before him said).
and player
knows
for all
. Show a protocol for all players, except the first to get the answer right?
could simply declares
where
stands for XOR. Now, player
can for example reconstruct
by
. Now, player
can do the same computation and figure out
. Now, he can calculate
and so on… When we move to an infinite number of players, however, we can’t do that anymore because taking the XOR of an infinite number of bits is not well defined. However, we can still can solve Puzzles #1 and #2 if we believe and are willing to accept the Axiom of Choice.
there is a set
such that
, i.e. a set that takes a representative from each element in the family.
that is shift invariant (say under addition modulo
) and
. The proof goes the following way: define the following equivalence relation on
:
if
. Now, consider the family of all the equivalence classes and invoke the Axiom of Choice. Let
be the set obtained. Now, we can write the interval as a disjoint union:
and
. Since it is an enumerable union, if such a measure existed, then:
which is either
if
or
if
.
be the set of all infinite
-strings and consider the equivalence relation on
such that
if the strings differ in a finite number of positions. Now, invoke the axiom of choice in the equivalence classes and let
be the set of representatives. Now, if
is the set of all strings with finite number of
‘s and
the operation such that
if
. We can therefore write:
they the entire string is. Now, they take
the representative of this class and guess
. Notice that
will differ from the real string by at most a finite number of bits.
simply looks at
and figure out the equivalence class he is and let
be the representative of this class. Now, since
and
differ by a finite number of bits, he can simply calculate XOR of
and
(now, since it is a finite number of them, XOR is well defined) and announce it. With this trick, it just becomes like Puzzle #0.
