Bimatrix games

May 25th, 2011 renatoppl No comments

This week in Israel is the Workshop on Innovations in Algorithmic Game Theory, which has been a collection of amazing talks and I thought of blogging about something new I learned here. First, Paul Goldberg gave an amazing talk about the Lemke-Howson algorithm and Homotopy Methods. Later, during the poster session Jugal Garg presented the impressive work on an exact algorithm for finding Nash equilibria in rank 1 bimatrix games. Both have in common the use of homotopy, which I found I quite cool idea – and has been present in Game Theory for a while, but I didn’t know about. They also have to do with improving the understanding we have on the Lemke-Howson Algorithm – a (potentially exponential time) algorithm to find Nash equilibrium in 2-person bi-matrix games, but that seems to work pretty well in practice. As always, I though that blogging about it would be a good idea in order to understand those concepts well.

Bimatrix Game and How to compute equilibrium

Bimatrix game is the simplest class of games studied. Basically it is a $2$ player game, with $n$ strategies for player $1$ and $m$ strategies for player 2 which is represented by a pair of $n \times m$ matrices $(A,B)$ . Let $x \in \mathbb{R}_+^n, \Vert x \Vert_1 = 1$ represent a probability distribution that player $1$ assigns to his strategies and $y \in \mathbb{R}_+^m, \Vert y \Vert_1 = 1$ be the same for player $2$ . This way, the players experience utilities:

$[; u_1 (x,y) = x^t A y,Â u_2(x,y) = x^t B y;]$

The best understood class of those games is the one where $A+B = 0$ , called zero-sum games. For this class, computing a Nash equilibrium is very easy and it is given by the famous min-max theorem: player $1$ finds $x$ maximizing $\min_j (x^t A e_j)$ where $e_j$ is the $j$ -th unit vector. Similarly player $2$ finds $y$ maximizing $\min_i (e_i^t B y)$ . Then the pair of strategies obtained is a Nash equilibrium – and this verifying that is not hard.

When $A+B \neq 0$ , the problems gets a lot more complicated. Proving that equilibrium exist can be done using various fixed point theorems, as Brouwer or Kakutani. There is a very simple exponential time algorithm for finding it and the key observation is the following, if $(x,y)$ is a Nash equilibrium then:

$\forall i: x_i = 0 \text{ or } \forall i': e_i^t A y \geq e_{i'}^t A y$

$\forall j: y_j = 0 \text{ or } \forall j': x^t B e_j \geq x^t B e_{j'}$

which means that each strategy for player $i$ is either in the support or is a best response. Proving that is trivial (if some strategy is in the support and is not a best response, then reducing the probability we play it is an improving deviation). Therefore if we just guess the support of $x$ and the support of $y$ we just need to find some strategies with this support satisfying the inequalities above. This can be done using a simple LP. This is clearly not very efficient, since it involves solving $2^{n+m}$ LPs. A still exponential, but a lot more practical method, is:

Lemke-Howson Algorithm

A good overview of the L-H algorithm can be found in those lecture notes or in a more detailed version in third chapter of the AGT book (a pdfÂ can be found in Tim’s website). Here I’ll present a quick overview. The main idea is to define the best-response polytopes $P$ and $Q$ :

$[; P = \{(x,v) \in \mathbb{R}^{n+1} \vert x_i \geq 0, x^t B e_j \leq v; \textbf{1}^t x = 1 \};]$

$[; Q = \{(y,u) \in \mathbb{R}^{m+1} \vert e_i^t A y \leq u, y_j \geq 0; \textbf{1}^t y = 1 \} ;]$

The intuition is that a point $(x,v) \in P$ represents the fact that the payoff $v$ of player $2$ when player $1$ plays $x$ is at least $v$ . We could re-write as $v \geq \max_j x^t B e_j$ .

Each of the polytopes has $m+n$ inequalities and $1$ equality. Given $x$ we define $L(x)$ as the indices of the tight inequalities in $P$ and similarly we define $L(y)$ as the indices of the tight inequalities in $Q$ . The theorem in the previous section can be rephrased as:

$(x,y)$ is Nash equilibrium iff $L(x) \cup L(y) = \{1, 2, \hdots, n+m\}$

So we need to look at points in the polytope below that are fully-labeled. And the way that this is done in L-H is quite ingenious – it is a similar idea that is used by the Simplex Method – walking through the vertices of the polytope looking for the desired vertex. In order to do it, let’s define another polytope:

$[;P' = \{x \in \mathbb{R}^n \vert x_i \geq 0, x^t B e_j \leq 1\} ;]$

$[;Q' = \{y \in \mathbb{R}^m \vert e_i^t A y \leq 1, y_j \geq 0\} ;]$

Note that there is a clear bijection between $P' \setminus 0 \leftrightarrow P$ and $Q' \setminus 0 \leftrightarrow Q$ . This is a projective transformation given by $x \mapsto (\frac{x}{\Vert x \Vert_1},\Vert x \Vert_1)$ . Notice that the labels are preserved by this transformation and the vertex and edges of the polytope are mapped almost 1-1 (except the vertex $0$ ). Notice a couple of details:

1. A vertex in $x \in P'$ corresponds to a point with $n$ labels. A vertex in $y \in Q''$ corresponds to a point with $m$ labels.

2. The point $(0,0)$ corresponds to a fully-labeled point of $P' \times Q'$ , unfortunately this is the only fully-labeled point that doesn’t correspond to a Nash equilibrium.

3. By taking an edge of the polytope (which is define by $n-1$ labels in $P'$ and $m-1$ labels in $Q'$ . We can move between two nodes that are almost fully labeled.

The idea is to consider the set of nodes that are almost fully-labeled: fix some label $k$ and consider all the nodes such that $L(x) \cup L(y) \supseteq \{1 .. k-1, k+1 .. n+m\}$ . Those points are either $(0,0)$ , a Nash equilibrium or they have one duplicated label, since $\vert L(x) \vert + \vert L(y) \vert = n+m$ . An edge is composed of $n+m-1$ labels (no duplicated labels). So, one almost fully-labeled point that is not a Nash or $(0,0)$ is only connected to two other vertices via an edge (which correspond to dropping one of the duplicated labels and following the corresponding edge).

This gives us a topology of the space of Nash equilibria. This tells us a couple of facts: (1) we can find a Nash equilibrium by starting in $(0,0)$ and following the L-H path. In the end of the path, we must find a Nash equilibrium. (ii) If the polytope is not degenerate, then there is an odd number of Nash equilibria and they are connected by L-H edges in the following way:

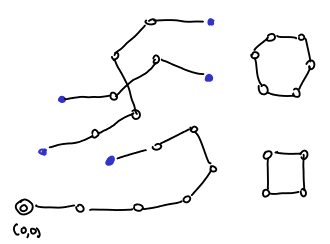where the blue dots are the Nash equilibria, the white dots are the almost fully-labeled points and the edges are the L-H edges. The number of Nash equilibria are odd by a simple parity argument.

The classic way in which simplex-like methods walk through the vertices of a polytope is by pivoting. The same way we can implement Lemke-Howson. For an explanation on the implementation, please look at the chapter 3 of the AGT book.

One can ask if we could modify the L-H path following to go through the path faster. Recently, Goldberg, Papadimitriou and Savani proved that finding the Nash equilibrium that L-H outputs is PSPACE-complete. So, in principle, finding this specific equilibrium, seems harder than finding any Nash, which is PPAD-complete.

My current plan is on some other blog posts on Bimatrix games. I wanted to discuss two things: first the homotopy methods and homotopy fixed-point-theorems (which is the heart of the two papers mentioned above) and about new techniques for solving zero-matrix where the strategy space is exponential.

Categories: theory Tags: algorithms, game theory, linear algebra

DP and the ErdÅ‘sâ€“RÃ©nyi model

May 16th, 2011 renatoppl No comments

Yesterday I was in a pub with Vasilis Syrgkanis and Elisa Celis and we were discussing about how to calculate the expected size of a connected component in $G(n,p)$ , the ErdÅ‘sâ€“RÃ©nyi model. $G(n,p)$ is the classical random graph obtained by considering $n$ nodes and adding each edge $(i,j)$ independently with probability $p$ . A lot is known about its properties, which very interestingly change qualitatively as the value of $p$ changes relativeto $n$ . For example, for $p <\frac{1}{n}$ then there is no component greater than $O(\log n)$ with high probability. When $p = \frac{c}{n}$ , $c>1$ and $n \rightarrow \infty$ , then the graph has a giant component. All those phenomena are very well studied in the context of probabilistic combinatorics and also in social networks. I remember learning about them in Jon Kleinberg’s Structure of Information Networks class.

So, coming back to our conversation, we were thinking on how to calculate the size of a connected component. Fix some node $u$ in $G(n,p)$ – it doesn’t matter which node, since all nodes are equivalent before we start tossing the random coins. Now, let $C_u$ be the size of the connected component of node $u$ . The question is how to calculate $C(n,p) = \mathbb{E} [C_u]$ .

Recently I’ve been learning MATLAB (actually, I am learning Octave, but it is the same) and I am very amazed by it and impressed about why I haven’t learned it before. It is a programming language that somehow knows exactly how mathematicians think and the syntax is very intuitive. All the operations that you think of performing when doing mathematics, they have implemented. Not that you can’t do that in C++ or Python, in fact, I’ve been doing that all my life, but in Octave, things are so simple. So, I thought this was a nice opportunity for playing a bit with it.

We can calculate $C(n,p)$ using a dynamic programming algorithm in time $O(n^2)$ – well, maybe we can do it more efficiently, but the DP I thought was the following: let’s calculate $\mathcal{C}(n,s,p)$ where it is the expected size of the $u$ -connected component of a random graph with $n$ nodes where the edges between $u$ and other nodes have probability $p' = 1 - (1-p)^s$ and an edge between $v_1$ and $v_2$ have probability $p$ . What we want to compute is $C(n,p) = \mathcal{C}(n,1,p)$ .

What we can do is to use the Principle of Deferred Decisions,Â and toss the coins for the $n-1$ edges between $u$ and the other nodes. With probability $bin(k,n,p') = {n \choose k} (p')^k (1-‘p)^{n-k}$ , there are $k$ edges between $u$ and the other nodes, say nodes $w_1, \hdots, w_k$ . If we collapse those nodes to $u$ we end up with a graph of $n-k$ nodes and the problem is equivalent to $k$ plus the size of the connected component of $u$ in the collapsed graph.

One difference, however is that the probability that the collapsed node $u$ is connected to a node $v$ of the $n-1-k$ nodes is the probability that at least one of $w_i$ is connected to $v$ , which is $1-(1-p)^k$ . In this way, we can write:

$\mathcal{C}(n,s,p) = 1 \cdot bin(0,n-1,p') + \sum_{k=1}^{n-1} bin(k,n-1,p') [ k + \mathcal{C}(n-k,k,p)]$

where $p' = 1-(1-p)^s$ . Now, we can calculate $C(n,p)$ by using DP, simply by filling an $n \times n$ table. In Octave, we can do it this way:


function component = C(N,p)
  C_table = zeros(N,N);
  for n = 1:N for s =1:N
    C_table(n,s) = binopdf(0,n-1,1-((1-p)^s)) ;
    for k = 1:n-1
      C_table(n,s) += binopdf(k,n-1,1-((1-p)^s)) * (k + C_table(n-k,k));
    end
  end end
  component = C_table(N,1);
endfunction

And in fact we can call $C(n,p)$ for say $n = 200$ and $p = 0.01 .. 0.3$ and see how $C(n,p)$ varies. This allows us, for example, to observe the sharp transition that happens before the giant component is formed. The plot we get is:

ErdÅ‘sâ€“RÃ©nyi model

Categories: theory Tags: probability

Reasoning about Knowledge

April 16th, 2011 renatoppl No comments

Last week, I went to Petra in Jordan together with Vasilis Syrgkanis and in the road we kept discussing about the Blue-Eyed Islanders Puzzle, posted by Terry Tao on his blog. It is a nice puzzle because it allows us to reflect on how to think about knowledge and how to make statements like “A knows that B knows that C doesn’t know fact F”. My goal in this post is not to discuss about the puzzle itself, but about a framework that allows us to think about it in a structured way. Nevertheless, I strongly recommend the puzzle, first because it is a lot of fun, and second, because it gives a great non-trivial example to think about this kind of thing. But first, a photo from Petra:

And then some references:

Classic: “Agreeing to Disagree” (Robert Aumann)
Survey:Â “Common Knowledge” (John Geanakoplos)
Book: “Reasoning about Knowledge” (Fagin, Halpern, Moses, Vardi)

I first read Aumann’s classic, which is a very beautiful and short paper — but where I got most intuition (and fun) was reading Chapter 2 of Reasoning About Knowledge.Â So, I’ll show here something in between of what Chapter 2 presents and what Geanakoplos’ survey presents (which is also an amazing source).

We want to reason about the world and the first thing we need is a set $\Omega$ representing all possible states the world can take. Each $\omega \in \Omega$ is called a state of the world and completely described the world we are trying to reason about. To illustrate the example, consider the situation where there are $n$ people in a room and each person has a number $x_i \in \{0,1\}$ in his head. Person $i$ can see the number of everyone else, except his. We want to reason about this situation, so a good way to describe the world is to simply define $\Omega = \{0,1\}^n$ of all $0,1$ -strings. We define an event to be simply a subset of the possible states of the world, i.e., some set $E \subseteq \Omega$ . For example, the even that player $1$ has number $0$ in his head is simply: $E = \{ x \in \Omega; x_1 = 0 \}$ . We could also think about the event $E'$ that the sum of the numbers is odd, which would be: $E' = \{ x \in \Omega; \sum_i x_i \text{ mod } 2 = 1 \}$ . Now, we need to define what it means for some person to know some event.

For each person $i$ , his knowledge structure is defined by a partition $P_i$ ofÂ $\Omega$ . The rough intuition is that player $i$ is unable to distinguish two elements $\omega_1, \omega_2$ in the same cell of partition $P_i$ . For each $\omega$ , $P_i(\omega)$ is the cell of partition $P_i$ containing $\omega$ . The way I see knowledge representation is that if $\omega$ is the true state of the world, then person $i$ knows that the true state of the world is some element in $P_i(\omega)$ .

Definition: We say that person $i$ knows event $E$ on the state of the world $\omega$ is $P_i(\omega) \subseteq E$ . Therefore, if person $i$ knows event $E$ , the world must be in some state $K_i(E) := \{\omega \in \Omega; P_i(\omega) \subseteq E\}$ .

Above we define the knowledge operator $K_i(\cdot)$ . Below, there is a picture in which we represent its action:

Now, this allows us to represent the fact that person $1$ knows that person $2$ knows of event $E$ as the event $K_1(K_2(E))$ . Now, the fact the person $1$ knows that person $2$ doesn’t know that person $1$ knows event $E$ can be represented as: $K_1(\neg K_2(K_1(E)))$ , where $\neg E := \Omega \setminus E$ .

An equivalent and axiomatic way of defining the knowledge operator is by defining it as an operator $K_i: 2^\Omega \rightarrow 2^\Omega$ such that:

$K_i(\Omega) = \Omega$
$K_i(A) \cap K_i(B) = K_i(A \cap B)$
$K_i(A) \subseteq A$
$K_i(K_i(A)) = K_i(A)$
$\neg K_i(A) = K_i(\neg K_i(A))$

Notice that axioms 1-4 define exactly a topology and together with 5 it is a topology that is closed under complement. The last two properties are more interesting: they say that if player $i$ knows something, then he knows that he knows and if the doesn’t know something, he knows that he doesn’t know. Aumann goes ahead and defines the notion of common knowledge:

Definition: We say that an event $E$ is common knowledge at $\omega$ if for any $k$ and for any sequence $i(1), \hdots, i(k)$ where $i(j)$ are players, then $\omega \in K_{i(1)} K_{i(2)} \hdots K_{i(k)} E$ .

Suppose that $P'$ is a partition that is a simultaneous coarsening of $P_1, \hdots, P_k$ , then for all cells $C$ of this partition, either $C$ or $\neg C$ is common knowledge.

An alternative representation is to represent $\Omega$ as nodes in a graph and add an edge between $\omega_1$ and $\omega_2$ labeled with $i$ if they are in the same cell of $P_i$ . Now, given the true state of the world $\omega \in \Omega$ , one can easily calculate the smallest event $E$ such that $i$ knows $E$ : this is exactly the states that are reached from $\omega$ just following edges labeled with $i$ , which is easily recognizable as $P_i(\omega)$ .

Now, what is the smallest set that $1$ knows that $2$ knows ? Those are the elements that we can arrive from a path following first an edge labeled $1$ and then an edge labeled $2$ . Extending this reasoning, it is easy to see that the smallest set that is common knowledge at $\omega$ are all the elements reachable from some path in this graph.

More about knowledge representation and reasoning about knowledge in future posts. In any case, I can’t recommend enough the references above.

Categories: theory Tags: knowledge, logic

Newer Entries Older Entries

Big Red Bits

Archive

Bimatrix games

DP and the ErdÅ‘sâ€“RÃ©nyi model

ErdÅ‘sâ€“RÃ©nyi model

Reasoning about Knowledge

Recent Posts

Archives

Categories

Comics

Systems Links

Theory Links

Meta