Walrasian Equilibrium I
Currently I’ve been trying to understand more about the dynamics of markets and basic concepts of microeconomic theory and, as always, writing a blog post will help me to keep my ideas clear. First, why are markets interesting from a computer scientist/mathematician point of view?
- Markets are multi-objective optimization problems: one can think of the possible state of a market some point in a space of possible
. Each player of the market controls one variable, say
and is interested in maximizing one objective function
. So, player
is trying to set
.
- Markets are a computational model: one can think of a market as a way of performing a certain computation – as extracting some kind of information, as a prediction market, stock exchanges, … If we think of it as a computational device, we are asking the same questions: given those preferences which are implicit functions to each of the agents, calculate “fair” prices of items.
- Markets are distributed systems where each part of the system has a selfish interest.
A market is composed by a set of commodities,
of consumers and
of producers. Now, we describe how to characterize each of them:
- Each consumer is defined by a set
of commodities combinations he is interested (typically we take
) and an utility function
expressing his interest for this bundle of commodities. Consumer
will try to maximize
in a further restricted
.
- Each producer is define by a set
it has the capacity to produce.
- Endowments: Each consumer comes to the market with an initial endowment
, so for
,
is the amount of commodity
that consumer
originally has. The initial total endowment of the market is given by
, which is a vector indicating how much of each commodity originally exists in the market.
- Shares: consumers have shares in the companies, so for
,
, consumer
has
shares of company
, such that
.
Something very crucial is missing in this picture: a way to compare commodities and something that makes exchanges possible: the answer to that is to attribute prices to the items. How to attribute prices to the items so that the market works fine? A price vector is a vector . Consider the following scenario after prices
are established to commodities:
- by producing
, company
gets profit
, so each company will try to maximize its profit producing
.
- each consumer sells its initial endowment and gets the profit respective to the companies he owns. So, consumer
gets
.
- now consumer
uses the money he has to buy the best bundle he can afford, which is
.
The amount of commodities in the market must conserve, so that is possible only if we get:
First, it is not clear if such a price vector exists. If it exists, is it unique? If this is an equilibrium, is it the best thing for the consumers? How those prices can be set in practice without a centralized authority? Can people lie? Below, let’s collect a couple of questions I’ll try to answer (yes, no or unknown) in this and the following posts.
Question 1: Does a price vector always exist that generates an equilibrium?
Question 2: If it exists, is it unique?
Question 3: Can we describe an efficent method to find ?
Question 4: Is it the best thing for the consumers in the following sense: if is an equilibrium, are there feasible
such that
and for at least one consumer
? (This is called Pareto improvement)
Question 5: A central authority could use the knowledge about functions and endowments
to calculate the price vector
using some method. Can consumers
be better off by lieing about their utility and endowments?
Question 6: How prices get defined without a central authority? Is there a dynamic/game-theoretical model to that?
For simplicity, let’s think of Exchange Economies, which are economies with no producers. Let’s define it formally:
Definition 1 An exchange economy is composed by a set of commodities
and a set of consumers
each with an utility
and an initial endowment
.
Definition 2 A price vector
is a Walrasian equilibrium for an exchange economy
if there is
such that:
s.t.

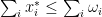
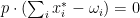
The first condition says that each consumer is maximizing his utility given his prices, the second says that we can’t buy more commodities than what is available in the market and the third, called Walras’ Law, says that if there is surplus of a certain product, it should have price zero. It is by far the most unnatural of those, but it can be easily justifiable in some circumnstances: suppose we say that utilities are non-satiated if for each and
, there is
,
such that
. If
are differentiable, that would mean
, for example a linear function
with some
. In that case,
and some player has money surplus and therefore he could increase his utility.
Now, we define for each price vector the excess demand function
and
. Now, under non-satiated utilities, by the last argument, we have that
is an equilibrium vector iff
. Actually, if
are also strong monotone, i.e.,
for each
, then it becomes:
is an equilibrium iff
, which means that the market clears:
The question that is easier to answer is Question 4 and it is sometimes refered as the First Fundamental Theorem of Welfare Economics:
Theorem 3 Given non-satiated preferences, each equilibrium
is Pareto, i.e. there is no other feasible allocation
such that for all
,
with the inequality strict for at least one component.
Proof: Suppose there were, since then
, because if
then we could improve the utility of
still within the budget, contradicting the optimality of
for that budget. And clearly
implies
.
Summing over , we get
, what is a contradiction, because since
is feasible,
and therefore
.
Now, let’s tackle Question 1. We assume linearly of utility: for
. This gives us strong monotonicity and local nonsatiated preferences.
Theorem 4 Under linear utilities, there is always an equilibrium price vector
.
Consider the function defined above:
where
is the bundle of best possible utility. Now, since we are using linear utilities we can’t guarantee there will be only one such bundle, so instead of considering a function, consider
and
as being correspondences:
, i.e.,
is the set of all allocations that maximize
subject to
. Since
are linear functionals, we can calculate
by a Fractional Knapsack algorithm: we sort commodities
by
and start buying in the cost-benefit order (the ones that provide more utility per buck spent). Most of the time there will be just one solution, but in points where
, then
might be a convex region. This correpondence is upper hemicontinuous, which is the correspondence analogue to continuity for functions. As Wikipedia defines:
Definition 5 A correspondence
is said to be upper hemicontinuous at the point
if for any open neighbourhood
of
there exists a neighbourhood
of a such that
is a subset of
for all
in
.
It is not hard to see that is upper hemicontinuous according to that definition. Our goal is to prove that there is one price vector
for which
or:
. To prove that we use Kakutani’s Fixed Point Theorem. Before we go into that, we’ll explore some other properties of
:
- 0-Homogeneous:
- Walras’ Law:
. For any
we know
by the definition of
. So, if it not zero, some
has money surplus what is absurd given that preferences are strongly monotone.
- Bounded:
is bounded from below, i.e.,
for some
. Simply take
- Boundary behavior: if
with
, then
. That is clear from the fractional knapsack algorithm when one desirable item gets price zero.
Now, we are in shape for applying Kakutani’s Fixed Point Theorem:
Theorem 6 (Kakutani, 1941) If
is an upper hemicontinuous correspondence such that
is a convex non-empty set for all
then
has a fixed point, i.e.,
s.t.
.
Since prices are -homogeneous, consider the simplex
, its relative interior
and the boundary
. Now we define the following price correcting correspondence
.
If some price is set, it generates demand
. For that demand, the price that would maximize profit would be
, i.e.
for all
. It is natural to re-adjust the prices to
. So we define for
:
and for :
Now, I claim that this correspondence satisfies the conditions in Kakutani’s Theorem. We skip a formal proof of this fact, but this is intuitive for the interior – let’s give the intuition why this is true as we approach the boundary: if
, then
, therefore the demans explodes:
and as a result the best thing to do is to set the prices of those commodities much higher than the rest. Therefore, the price of the commodities whose demand explode are positive while the prices of the commodities where the price doesn’t get value zero.
Now, after waiving our hands about the upper continuity of , we have by Kakutani’s Theorem a point
such that
. By the definition of
we must have
(because for
,
. Now, I claim
. In fact if
, still
by Walras’ Law. So, if
then there is
with
and therefore
for all
, and
. For this reason
.
In the next blog post (or serie of blog posts, let’s see) we discuss issues related to the other questions: uniqueness, dynamics, game-theoretical considerations, …