Bounded Degree Spanning Tree and an Uncrossing Lemma
I’ve been reading about the Bounded Degree Spanning Tree problem and I thought of writing some of what I am learning here. It illustrates a beautiful techique called Iterated Rounding and uses the combinatorial idea of uncrossing. I’ll try to give a high-level idea of the argument and give references on the details. The first result of this kind was given by Goemans (although there were previous results with weaker guarantees) by Goemans in Minimum Bounded Degree Spanning Trees, but the result based on iterated rounding and a subsequent improvement are due to Singh and Lau in a serie of papers. A main reference is Approximating minimum bounded degree spanning trees to within one of optimal.
The problem of bounded degree spanning tree is as follows: consider a graph with edge weights and we for some nodes
a degree bound
. We want to find, among the spanning trees for which the degree of
is
the one with minimum cost. It is clearly a hard problem, since taking all weights equal to
and
for all nodes is the Hamiltonian Path problem, which is NP-complete. We will get a different kind of approximation. Let OPT be the optimal solution: we will show an algorithm that gives a spanning tree of cost
such that each node
has degree
(this can be improved to
with a more sofisticated algorithm, also based on Iterated Rounding).
As always, the first step to design an approximation algorithm is to relax it to an LP. We consider the following LP:
The first constraint expresses that in a spanning tree, there are at most edges, the second prevent the formation of cycles and the third guarantees the degree bounds. For
we have the standard Minimal Spanning Tree problem and for this problem the polytope is integral. With the degree bounds, we lose this nice property. We can solve this LP using the Ellipsoid Method. The separation oracle for the
is done by a flow computation.
Iterated Rounding
Now, let’s go ahead and solve the LP. It would be great if we had an integral solution: we would be done. It is unfortunately not the case, but we can still hope it is almost integral in some sense: for example, some edges are integral and we can take them to the final solution and recurse the algorithm on a smaller graph. This is not far from truth and that’s the main idea of the iterated rounding. We will show that the support of the optimal solution has some nice structure. Consider the following lemma:
Lemma 1 For any basic solution
of the LP, either there is
with just one incident edge in the support
or there is one
such that that at most
edges are incident to it.
If we can prove this lemma, we can solve the problem in the following way: we begin with an empty tree: then we solve the LP and look at the support . There are two possibilities according to the lemma:
- If there is one node
with just one edge
incident to it in the support, we add it to the tree, remove
from
, decrease
, make
(the trick is to remove in each iteration edges from
that are not in the support. Clearly, removing those edges doesn’t hurt the objective value) and run the algorithm again. Notice that the LP called in the recursion has value less or equal then the actual LP
. So if by induction we get a spanning tree respecting the new degree bounds plus two and value less or equal than the new LP value, we can just add
and we have a solution with value less or equal than the one of the original LP respecting the degree bounds plus two.
- Otherwise, there is one node
that has degree
in the support. So, we just remove that degree bound on that vertex (i.e. remove
from
), make
(again,eliminate the edges not in the support) and run the algorithm again. Clearly, if one node is still in
, it has
, since there are only three edges in the support, there will be for the rest of the computation, just three edges incident to it, so there will be at most three edges more incident to it. So it will exceed its original
by at most
.
The algorithm eventually stops, since in each iteration we have less edges or less nodes in and the solution is as desired. The main effort is therefore to prove the lemma. But before, let’s look at the lemma: it is of the following kind: “any basic solution of the LP has some nice properties, which envolve having a not too big (at least in some point) support”. So, it involves proving that the support is not too large. That is our next task as we are trying to prove the lemma. And we will be done with:
Theorem 2 The algorithm described above produces a spanning tree of cost
(the LP values and therefore
)in which each node
has degree
.
Bounding the size of the support
We would like now to prove some result like the Lemma above: that in the solution of the LP we have either one with degree
in
or we have a node in
with degree
. First, we suppose the opposite, that
has all the nodes with degree
and all the nodes in
have degree
. This implies that we have a large number of edges in the support. From the degrees, we know that:
We want to prove that the support of the LP can’t be too large. The first question is: how to estimate the size of the support of a basic solution. The constraints look like that:
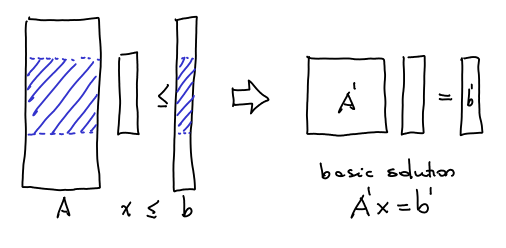
A basic solution can be represented by picking rows of the matrix and making them tight. So, if we have a general
LP, we pick some submatrix
of
which is
and the basic solution is just
. The lines of matrix
can be of three types: they can be
, which are corresponding to
,
that correspond to
or
corresponding to
. There are
vectors in total. The size of the support
is smaller or equal the number of rows of the form
in the basic solution. Therefore the idea to bound the size of the support is to prove that “all basic solutions can be represented by a small number of rows in the form
. And this is done using the following:
Lemma 3 Assuming
, for any basic solution
, there is
and a family
of sets such that:
- The restrictions correspondent to
and
are tight for

is an independent set
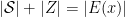
is a laminar family
The first 3 items are straightfoward properties of basic solutions. The fourth one, means that for two sets , one of three things happen:
,
or
. Now, we based on the previous lemma and in the following result that can be easily proved by induction, we will prove Lemma 1.
Lemma 4 If
is a laminar family over the set
where each set
contains at least
elements, then
.
Now, the proof of Lemma 1 is easy. Let’s do it and then we come back to prove Lemma 3. Simply see that what contradicts
.
Uncrossing argument
And now we arrive in the technical heart of the proof, which is proving Lemma 3. This says that given any basic solution, given any feasible solution, we can write it as a “structured” basic solution. We start with any basic feasible solution. This already satifies (1)-(3), then we need to change that solution to satisfy condition (4) as well. We need to get rid crossing elements, i.e., in the form:
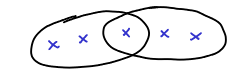
We do that by the means of the:
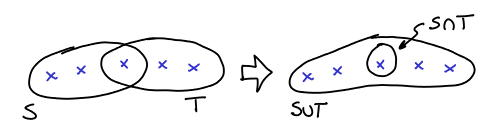
Lemma 5 (Uncrossing Lemma) If
and
are intersecting and tight (tight in the sense that their respective constraint is tight), then
and
are also tight and:
Which corresponds to that picture:
Proof: First, we note that is a supermodular function, i.e.:
We can see that by case analysis. Every edge appearing in the left side appears in the right side with at least the same multiplicity. Notice also that it holds with strict inequality iff there are edges from to
. Now, we have:
where the first relation is trivial, the second is by feasibility, the third is by supermodularity and the lastone is by tightness. So, all hold with equality and therefore and
are tight. We also proved that:
so there can be no edge from to
in
and therefore, thinking just of edges in
we have:
Uncrossing arguments are found everywhere in combinatorics. Now, we show how the Uncrossing Lemma can be used to prove Lemma 1:
Proof: Let be any basic solution. It can be represented by a pair
where
and
is a family of sets. We will show that the same basic solution can be represented by
where
is a laminar family and has the same size of
.
Let be all sets that are tight under
and
a maximal laminar family of tights sets in
, such that
are independent. I claim that
.
In fact, suppose , then there are sets of
we could add to
without violating independence – the problem is that those sets would cross some set. Pick such
intersecting fewer possible sets in
. The set
intersects some
. Since both are tight we can use the Uncrossing Lemma and we get:
since , we can’t have simultaneously
and
in
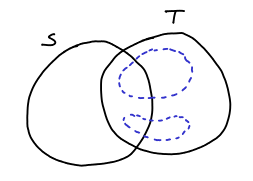
. Let’s consider two cases:
-
, then
is in
and intersects fewer sets of
than
, since all sets that intersect
in
must intersect
as well (since no set can cross
).
-
, then
is in
and intersects fewer sets of
than
, since all sets that intersect
in
must intersect
.
In either case we have a contradiction, so we proved that . So we can generate all the space of tight sets with a laminar family.
And this finishes the proof. Let’s go over all that we’ve done: we started with an LP and we wanted to prove that the support of each solution was not too large. We wanted that because we wanted to prove that there was one node with degree one in the support or a node in with small (
) degree. To prove that the degree of the support is small, we show that any basic solution has a representation in terms of a laminar family. Then we use the fact that laminar families can’t be very large families of sets. For that, we use the celebrated Uncrossing Lemma.
Note: Most of this is based on my notes on David Williamson’s Approximation Algorithms class. I spent some time thinking about this algorithm and therefore I decided o post it here.