Archive

Posts Tagged ‘puzzles’

Hats, codes and puzzles

October 3rd, 2009 No comments

When I was a child someone told me the following problem:

A king promised to marry his daughter to the most intelligent man. Three princes came to claim her hand and he tryed the following logic experiment with them: The princes are gathered into a room and seated in a line, one behind the other, and are shown 2 black hats and 3 white hats. They are blindfolded, and 1 hat is placed on each of their heads, with the remaining hats hidden in a different room. The first one to deduce his hat color will marry the princess. If some prince claims his hat color incorrectly he dies.

The prince who is seated behind removes his blindfold, sees the two hats in front of him and says nothing. Then the prince in the middle removes his blindfold after that and he can see the hat of the prince in front of him. He also says nothing. Noticing the other princes said nothing, the prince seated in the first whole, without even removing his blindfold, gives the correct answer? The question is: what is the color he said?

This is a simple logical puzzle: we just write all the possibilities and start ruling them out given that the other princes didn’t answer and in the end we can find the color of his hat. I remember that this puzzle surprised me a lot as a kid. A found it extremly cool by then, what made me want to read books about logic problems. After that, I had a lot of fun reading the books by Raymond Smullyan. I usually would read the problems, think something like: there can’t ba a solution to that. Then go to school with the problem in mind and spend the day thinking about that. Here is a problem I liked a lot:

There is one prisoner and there are two doors: each has one guardian. One door leads to an exit and one door leads to death. The prisioner can choose one door to open. One guardian speaks only the truth and one guardian always lies. But you don’t know which door is which, which guardian is which and who guards each door. You are allowed to choose one guardian and make him one Yes/No question, and then you need to choose a door. What is the right question to ask?

hats1

But my goal is not to talk about logic puzzles, but about Hat problems. There are a lot of variations of the problems above: in all of them a person is allowed to see the other hats but not his own hat and we need to “guess” which is the color of our hat. If we think carefully, we will see that this is a very general kind of problem in computer science: (i) the whole goal of learning theory is to predict one thing from a lot of other things you observe; (ii) in error correcting code, we should guess one bit from all the others, or from some subset of the others; (iii) in universal truthful mechanisms, we need to make a price offer to one player that just depends on all other players bids. I’ll come back to this example in a later post, since it is what made me interested in those kinds of problems, but for now, let’s look at one puzzle I was told about by David Malec at EC’09:

There are black and white hats and {3} people: for each of them we choose one color independently at random with probability {\frac{1}{2}}. Now, they can look at each others hats but not at their own hat. Then they need to write in a piece of paper either “PASS” or one color. If all pass or if someone has a wrong color, the whole team loses (this is a team game) and if at lest one person gets the color right and no one gets wrong, the whole team wins. Create a strategy for the team to win with {\frac{3}{4}} probability.

To win with {\frac{1}{2}} probability is easy: one person will always write “BLACK” and the others “PASS”. A better strategy is the following: if one person sees two hats of equal color, he writes the opposite color, otherwise, he passes. It is easy to see the team wins except in the case where all hats are the same color, what happens with {\frac{1}{4}} probability. We would like to extend this to a more general setting:

There are black and white hats and {2^k - 1} people: for each of them we choose one color independently at random with probability {\frac{1}{2}}. Now, they can look at each others hats but not at their own hat. Then they need to write in a piece of paper either “PASS” or one color. If all pass or if someone has a wrong color, the whole team loses (this is a team game) and if at lest one person gets the color right and no one gets wrong, the whole team wins. Create a strategy for the team to win with {1-\frac{1}{2^k}} probability.

It is a tricky question on how to extend the above solution in that case. A detailed solution can be found here. The idea is quite ingenious, so I’ll sketch here. It envolves Error Correcting Code, in that case, the Hamming Code. Let {F = \{0,1\}} with sum and product modulo {2}. Let {w_1, \hdots, 2^{2^k-1}} be the non-zero vector of {F^k} and the following linear map:

\displaystyle \begin{aligned} \phi: F^{2^k-1} \rightarrow F^k \\ (a_1,\hdots, a_{2^k-1}) \mapsto \sum_i a_i w_i \end{aligned}

Let {H} be the kernel of that application. Then, it is not hard to see that {H, H+e_1, \hdots, H+e_{2^k-1}} is a partition of {F^{2^k-1}} and also that because of that fact, for each {x \in F^{2^k-1}} either {x \in H} or exists a unique {i} s.t. {x + e_i \in H}. This gives an algorithm for just one player to guess his correct color. Let {x \in F^{2^k-1}} be the color vector of the hats. Player {i} sees this vector as:

\displaystyle (x_1, \hdots, x_{i-1}, ?, x_{i+1}, \hdots, x_n)

which can be {(x_1, \hdots, x_{i-1}, 0, x_{i+1}, \hdots, x_n)} or {(x_1, \hdots, x_{i-1}, 1, x_{i+1}, \hdots, x_n)}. The strategy is: if either one of those vector is in {H}, write the color corresponding to the other vector. If both are out of {H}, pass. The team wins iff {x \notin H}, what happens with {1 - \frac{1}{2^k}} probability. Is is an easy and fun exercise to prove those facts. Or you can refer to the solution I just wrote.

hats2

Now, we can complicate it a bit more: we can add other colors and other distributions. But I wanted to move to a different problem: the paper Derandomization of Auctions showed me an impressive thing: we can use coding theory to derandomize algorithms. To illustrate their ideas, they propose the following problem:

Color guessing problem: There are {n} people wearing hats of {k} different colors. If each person can see everyone else’s hats but not his or her own. Each person needs to guess the color of his own hat. We want a deterministic guessing algorithm that {1/k} fraction of each color class is guessed correctly.

The problem is very easy if we have a source of random bits. Each person guesses some color at random. It seems very complicated to do that without random bits. Surprisingly, we will solve that using a flow computation:

Let {c = (c_1, \hdots, c_n)} be an array of colors {c_{-i}} the array with color {i} removed. Consider the following flow network: nodes {s} and {t} (source and sink), nodes {v_{c_{-i}}} for each {c_{-i}}. There are {n \cdot k^{n-1}} such nodes. Consider also nodes in the form {u_{\gamma, c})} where {\gamma} is a color ({1, \hdots, k}) and {c} is a color vector. There are {k^{n+1}} such nodes.

hats_net

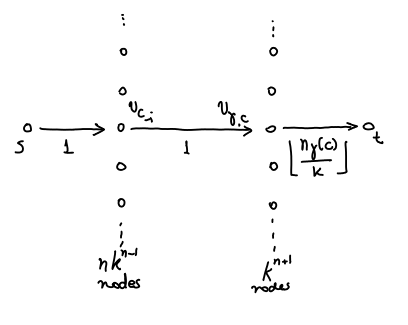
We have edges from {s} to {v_{c_{-i}}} for all nodes of that kind. And we have edges from {u_{\gamma, c})} to {t}. Now, if {c = (\gamma, c_{-i})}, i.e., if {c_{-i}} completed in the {i}-th coordinate with {\gamma} generates {c}, then add an edge from {v_{c_{-i}}} to {u_{\gamma, c})}.

Consider the following flow: add {1} unit of flow from {s} to {v_{c_{-i}}} and from {v_{c_{-i}}} split that flow in pieces of size {1/k} and send each to {u_{\gamma, c}} for {c = (\gamma, c_{-i})}. Now, each node {u_{\gamma, c_{-i}}} receives {\frac{n_\gamma(c)}{\gamma}} flow, where {n_{\gamma}(c)} is the number of occurencies of {\gamma} in {c}. Send all that flow to {t}.

We can think of that flow as the guessing procedure. When we see {c_{-i}} we choose the guess independently at random and this way, each {c} receives in expectation {\frac{n_\gamma(c)}{\gamma}} guesses {\gamma}. Notice that an integral flow in that graph represents a deterministic guessing procedure: so all we need is an integral flow so that the flow from {u_{\gamma, c}} to {t} is {\lfloor n_\gamma (c) / k \rfloor }. The flow received is from nodes of the type: {v_{c_{-i}}} and that means that bidder {i} in {c}, looking at the other hats will correctly choose {c_i}, {\lfloor n_\gamma (c) / k \rfloor } times.

Now, define the capacities this way: for all edges from {s} to {v_{c_{-i}}} and from {v_{c_{-i}}} to {u_{\gamma, c}} have capacity {1} and from {u_{\gamma, c}} to {t} capacity {\lfloor n_\gamma (c) / k \rfloor }. There is an integral flow that saturates all edges from {u} to {t}, because of the fractional flow showed. So, the solution gives us a deterministic decision procedure.

In the next blog post, I’ll try to show the result in the Derandomization of Auctions that relates that to competitive auctions.

Categories: puzzles Tags: , , ,

Prisioners and boxes

July 13th, 2009 No comments

In EC, Sean, one of my friends from UBC, told me an interesting puzzle. I liked both the problem and the solution a lot and since the solution has a lot of interesting ideas, I felt like writing about it. EC also reminded me that puzzles are fun and that I should use a bit more of my time solving those nice math problems. The problem is like that:

There were 100 prisoners and 3 different rooms, say A, B and C. In the beginning they are all in room A. In room B there are 100 boxes, each one containing the name of a different prisoner. One at a time, the prisoners are brought from A to B and in B they can open 50 boxes. Then they are brought to room C. (They cannot change the state of room B, so it is the same of having 100 identical copies of room B and bringing each prisoner to one of the rooms. They cannot leave signals in the room). If each prisoner finds his owns name, they are all freed. They only think they can do is to agree on a certain strategy while they are all in room A and then follow that strategy. If they don’t succeed, the names are randomly rearranged and they can try again the next day. Find a strategy for them so that they succeed in less than one week (in expectation).

A few things I need to drawn your attention to: (i) it is purely a math puzzle, there are no word-games. If something is obscure, it was my fault and it was not intentional, (ii) the fact that names were rearranged in boxes randomly is very important. The solution doesn’t work if the distribution is adversarial. (iii) if each of them pick 50 boxes at random, than each prisioner has 1/2 probability of succeeding, so they take 2^{100} days in expectation, what is a lot. How to reduce it to about seven days?

Structure of random permutations

The solution has to do with the structure of a permutation drawn at random. Consider one of the n! permutation is sampled uniform at random. We can write each permutation as a product of disjoint cycles. For example, the permutation \sigma = \begin{pmatrix} 1&2&3&4&5&6\\4&5&6&3&2&1 \end{pmatrix} can be written as a product of two disjoint cycles: \sigma = ( 1,4,3,6 ) (2,5). In the language of boxes and prisoners, it is: box a_1 contains the name of prisoner a_2, then box a_2 contains the name of prisoner a_3 and so on, until box a_k contains name of prisoner a_1. This is the cycle (a_1, a_2, \hdots, a_k). If  all the cycles have length smaller than n/2 where n is the number of prisoners, then there is a simple strategy: we can consider that each prisoner corresponds to one box a priori (say prisoners have number 1, \hdots, n and boxes also have numbers 1, \hdots, n. The permutation  is define by the function \sigma from the box number to the number of the prisoner whose name is inside the box. Now, prisoner k opens box k, reads the name of the prisoner inside the box and the box with that number, then he looks at the number of the prisoner inside that other box and continues following the cycle.

The probability of success is the same of the probability that a permutation \pi drawn at random has no cycle of size greater than n/2. Let $\phi_p$ be the probability that a random permutation has a cycle of length p, where p > n/2. This is a simple exercise of combinatorics: we can have \begin{pmatrix} n \\ p \end{pmatrix} ways of picking the p elements that will form the p-cycle. There are (n-p)! permutations for the remaining n-p elements and (p-1)! cycles that can be formed with those p elements. So, we have:

\displaystyle \phi_p = \frac{1}{n!} \begin{pmatrix} n \\ p \end{pmatrix} (n-p)! (p-1)! = \frac{1}{p}

And therefore the probability of having a cycle with length more than n/2 is \sum_{p=1+n/2}^n \frac{1}{p}. For n = 100, we get about 0.68, therefore the expected time before one permutation with no cycle larger than n/2 appears is \frac{1}{1-0.68} \approx 3.3 days. Much less than one week, actually!

Structure and Randomness

The solution to this puzzle explores the structure in randomness. A lot of work in computer science is based on looking at the structure (or expected structure) of a randomly chosen object. A very elegant kind of proof consists in creating a random process that generates object and prove that some object exists because is happens with positive probability. One simple, yet very beautiful example, is the following theorem: given any logic expression in 3-CNF form, i.e., one expression of the kind:

\displaystyle \bigwedge_i (a_{i1} \vee a_{i2} \vee a_{i3})

where a_{ij} \in \{ x_i, \tilde x_i\}, there is an assignment of x_i to \{0,1\} that satisfies 7/8 of the clauses. Even though the statement of this result has no probability in it, the proof is probabilitic. Consider a random assignment to the variables. Then each clause is satisfied with probability 7/8. Because of linearity of expectation, the expected number of satisfied clauses is 7/8 of the total. Since this is the expected number of satisfied clauses, there must be at least one assignments satisfying more than 7/8.

This kind of proof is called the probabilistic method. There are also a lot of other cool things exploring randomness in computer science, in design of algorithms, criptography, complexity theory, … Recently I read a nice blog post by Lipton, he discusses ways he would try to solve the P vs NP problem. One comment I found really interesting and exciting (but that I don’t quite understand yet) is that we could, maybe, separate the SAT-3 instances in “random” and “structured” instances and try to use different methods exploring randomness or structure in each of them.

\left(\begin{array}{ccc}1&2&3\\3&2&1\end{array}\ri  ght)

Categories: puzzles Tags: , ,