This week I will present the Theory Discussion Group about Competitive Auctions. It is mainly a serie of results in papers from Jason Hartline, Andrew Goldberg, Anna Karlin, Amos Fiat, … The first paper is Competitive Auctions and Digital Goods and the second is Competitive Generalized Auctions. My objective is to begin with a short introduction about Mechanism Design, the concept of truthfulness and the characterization of Truthful Mechanisms for Single Parameter Agents. Then we describe the Random Sampling Auction for Digital Goods and in the end we discuss open questions. I thought writting a blog post was a good way of organizing my ideas to the talk.
1. Mechanism Design and Truthfulness
A mechanism is an algorithm augmented with economic incentives. They are usually applied in the following context: there is an algorithmic problem and the input is distributed among several agents that have some interest in the final outcome and therefore they may try manipulate the algorithm. Today we restrict our attention to a specific class of mechanisms called single parameter agents. In that setting, there is a set  consisting of
consisting of  agents and a service. Each agent
agents and a service. Each agent  has a value
has a value  for receiving the service and
for receiving the service and 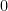 otherwise. We can think of
otherwise. We can think of  as the maximum player
as the maximum player  is willing to pay for that service. We call an environment
is willing to pay for that service. We call an environment  the subsets of the bidders that can be simultaneously served. For example:
the subsets of the bidders that can be simultaneously served. For example:
- Single item auction:

- Multi item auction:

- Digital goods auction:
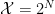
- Matroid auctions:
 is a matroid on
is a matroid on 
- Path auctions:
 is the set of edges in a graph and
is the set of edges in a graph and  is the set of
is the set of  -paths in the graph
-paths in the graph
- Knapsack auctions: there is a size
 for each
for each  and
and 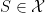 iff
iff 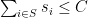 for a fixed
for a fixed 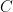
Most mechanism design problems focus in maximizing (or approximating) the social welfare, i.e., finding 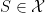 maximizing
maximizing  . Our focus here will be maximizing the revenue of the auctioneer. Before we start searching for such a mechanism, we should first see which properties it is supposed to have, and maybe even first that that, define what we mean by a mechanism. In the first moment, the agents report their valuations
. Our focus here will be maximizing the revenue of the auctioneer. Before we start searching for such a mechanism, we should first see which properties it is supposed to have, and maybe even first that that, define what we mean by a mechanism. In the first moment, the agents report their valuations  (which can be their true valuations or lies), then the mechanism decides on an allocation
(which can be their true valuations or lies), then the mechanism decides on an allocation  (in a possibly randomized way) and charges a payment
(in a possibly randomized way) and charges a payment 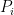 for each allocated agents. The profit of the auctioneer is
for each allocated agents. The profit of the auctioneer is 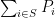 and the utility of a bidder is:
and the utility of a bidder is:
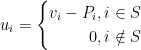
The agents will report valuations so to maximize their final utility. We could either consider a general mechanism e calculate the profit/social welfare in the game induced by this mechanism or we could design an algorithm that gives incentives for the bidders to report their true valuation. The revelation principle says there is no loss of generality to consider only mechanisms of the second type. The intuition is: the mechanisms of the first type can be simulated by mechanisms of the second type. So, we restrict our attention to mechanisms of the second type, which we call truthful mechanisms. This definnition is clear for deterministic mechanisms but not so clear for randomized mechanisms. There are two such definitions:
- Universal Truthful mechanisms: distribution over deterministic truthful mechanisms, i.e., some coins are tossed and based on those coins, we choose a deterministic mechanism and run it. Even if the players knew the random coins, the mechanism would still be truthful.
- Truthful in Expectation mechanisms: Let
 be the utility of agent
be the utility of agent  if he bids
if he bids 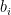 . Since it is a randomized mechanism, then it is random variable. Truthful in expectation means that
. Since it is a randomized mechanism, then it is random variable. Truthful in expectation means that ![{\mathop{\mathbb E}[u_i(v_i)] \geq \mathop{\mathbb E}[u_i(b_i)], \forall b_i} {\mathop{\mathbb E}[u_i(v_i)] \geq \mathop{\mathbb E}[u_i(b_i)], \forall b_i}](http://s0.wp.com/latex.php?latex=%7B%5Cmathop%7B%5Cmathbb+E%7D%5Bu_i%28v_i%29%5D+%5Cgeq+%5Cmathop%7B%5Cmathbb+E%7D%5Bu_i%28b_i%29%5D%2C+%5Cforall+b_i%7D&bg=T&fg=000000&s=0) .
.
Clearly all Universal Truthful mechanisms are Truthful in Expectation but the converse is not true. Now, before we proceed, we will redefine a mechanism in a more formal way so that it will be easier to reason about:
Definition 1 A mechanism  is a function that associated for each
is a function that associated for each  a distribution over elements of
a distribution over elements of  .
.
Theorem 2 Let ![{x_i(v) = \sum_{i \in S \in \mathcal{X}} Pr_{\mathcal{M}(v)}[S]} {x_i(v) = \sum_{i \in S \in \mathcal{X}} Pr_{\mathcal{M}(v)}[S]}](http://s0.wp.com/latex.php?latex=%7Bx_i%28v%29+%3D+%5Csum_%7Bi+%5Cin+S+%5Cin+%5Cmathcal%7BX%7D%7D+Pr_%7B%5Cmathcal%7BM%7D%28v%29%7D%5BS%5D%7D&bg=T&fg=000000&s=0) be the probability that
be the probability that  is allocated by the mechanism given
is allocated by the mechanism given  is reported. The mechanism is truthful iff
is reported. The mechanism is truthful iff  is monotone and each allocated bidder is charged payment:
is monotone and each allocated bidder is charged payment:

This is a classical theorem by Myerson about the characterization of truthful auctions. It is not hard to see that the auction define above is truthful. We just need to check that  for all
for all 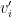 . The opposite is trickier but is also not hard to see.
. The opposite is trickier but is also not hard to see.
Note that this characterization implies the following characterization of deterministic truthful auctions, i.e., auctions that map each  to a set
to a set 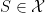 , i.e., the probability distribution is concentrated in one set.
, i.e., the probability distribution is concentrated in one set.
Theorem 3 A mechanism is a truthful deterministic auction iff there is a functions  such that for each we allocate to bidder
such that for each we allocate to bidder  iff
iff 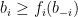 and in case it is allocated, we charge payment
and in case it is allocated, we charge payment  .
.
It is actually easy to generate this function. Given a mechanism, 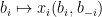 is a monotone and is a
is a monotone and is a  -function. Let
-function. Let  the point where it transitions from
the point where it transitions from 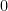 to
to  . Now, we can give a similar characterization for Universal Truthful Mechanism:
. Now, we can give a similar characterization for Universal Truthful Mechanism:
Theorem 4 A mechanism is a universal truthful randomized auction if there are functions  such that for each we allocate to bidder
such that for each we allocate to bidder  iff
iff 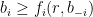 and in case it is allocated, we charge payment
and in case it is allocated, we charge payment  , where
, where  are random bits.
are random bits.
2. Profit benchmarks
Let’s consider a Digital Goods auction, where  . Two natural goals for profit extraction would be
. Two natural goals for profit extraction would be 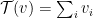 and
and 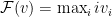 where we can think of
where we can think of  , the first is the best profit you can extract charging different prices and the second is the best profit you can hope to extract by charging a fixed price. Unfortunately it is impossible to design a mechanism that even
, the first is the best profit you can extract charging different prices and the second is the best profit you can hope to extract by charging a fixed price. Unfortunately it is impossible to design a mechanism that even  -approximates both benchmarks on every input. The intuition is that
-approximates both benchmarks on every input. The intuition is that 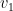 can be much larger then the rest, so there is no way of setting
can be much larger then the rest, so there is no way of setting  in a proper way. Under the assumption that the first value is not much larger than the second, we can do a good profit approximation, though. This motivates us to find an universal truthful mechanism that approximates the following profit benchmark:
in a proper way. Under the assumption that the first value is not much larger than the second, we can do a good profit approximation, though. This motivates us to find an universal truthful mechanism that approximates the following profit benchmark:

which is the highest single-price profit we can get selling to at least 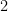 agents. We will show a truthful mechanism that
agents. We will show a truthful mechanism that 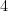 -approximates this benchmark.
-approximates this benchmark.
3. Profit Extractors
Profit extractor are building blocks of many mechanisms. The goal of a profit extractor is, given a constant target profit 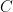 , extract that profit from a set of agents if that is possible. In this first moment, let’s see
, extract that profit from a set of agents if that is possible. In this first moment, let’s see 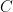 as an exogenous constant. Consider the following mechanism called CostShare
as an exogenous constant. Consider the following mechanism called CostShare : find the largest
: find the largest  s.t.
s.t. 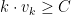 . Then allocate to
. Then allocate to
Lemma 5 CostShare is a truthful profit-extractor that can extract profit
is a truthful profit-extractor that can extract profit 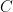 whenever
whenever 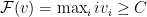 .
.
Proof: It is clear that it can extract profit at most 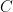 if
if 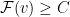 . We just need to prove it is a truthful mechanism and this can be done by checking the characterization of truthful mechanisms. Suppose that under CostShare
. We just need to prove it is a truthful mechanism and this can be done by checking the characterization of truthful mechanisms. Suppose that under CostShare exacly
exacly  bidders are getting the item, then let’s look at a bidder
bidders are getting the item, then let’s look at a bidder  . If bidder
. If bidder  is not getting the item, then his value is smaller than
is not getting the item, then his value is smaller than  , otherwise we could incluse all bidders up to
, otherwise we could incluse all bidders up to  and sell for a price
and sell for a price  for some
for some 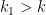 . It is easy to see that bidder
. It is easy to see that bidder  will get the item just if he changes his value
will get the item just if he changes his value  to some value greater or equal than
to some value greater or equal than  .
.
On the other hand, it  is currently getting the item under
is currently getting the item under  , then increasing his value won’t make it change. It is also clear that for any value
, then increasing his value won’t make it change. It is also clear that for any value  , he will still get the item. For
, he will still get the item. For 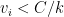 he doesn’t get it. Suppose it got, then at least
he doesn’t get it. Suppose it got, then at least  people get the item, because the price they sell it to
people get the item, because the price they sell it to  must be less than
must be less than 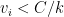 . Thefore, increasing
. Thefore, increasing  back to its original value, we could still sell it to
back to its original value, we could still sell it to  players, what is a contradiction, since we assumed we were selling to
players, what is a contradiction, since we assumed we were selling to  players.
players.
We checked monotonicity and we also need to check the payments, but it is straightforward to check they satisfy the second condition, since  for
for  and zero instead.
and zero instead. 
4. Random Sampling Auctions
Now, using that profit extractor as a building block, the main idea is to estimate 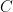 smaller than
smaller than 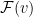 for one subset of the agents and extract that profit from them using a profit extractor. First we partition
for one subset of the agents and extract that profit from them using a profit extractor. First we partition  is two sets
is two sets  and
and 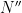 tossing a coin for each agent to decide in which set we will place it, then we calculate
tossing a coin for each agent to decide in which set we will place it, then we calculate  and
and 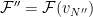 . Now, we run CostShare
. Now, we run CostShare and CostShare
and CostShare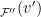 . This is called Random Cost Sharing Auction.
. This is called Random Cost Sharing Auction.
Theorem 6 The Random Cost Sharing Auction is a truthful auction whose revenue 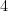 -approximates the benchmark
-approximates the benchmark  .
.
Proof: Let  be a random variable associated with the revenue of the Sampling Auction mechanism. It is clear that
be a random variable associated with the revenue of the Sampling Auction mechanism. It is clear that 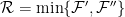 . Let’s write
. Let’s write 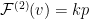 meaning that we sell
meaning that we sell  items at price
items at price 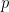 . Let
. Let  where
where  and
and  are the items among those
are the items among those  items that went to
items that went to  and
and 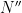 respectively. Then, clearly
respectively. Then, clearly  and
and 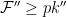 , what gives us:
, what gives us:

and from there, it is a straighforward probability exercise:
![\displaystyle \frac{\mathop{\mathbb E}[{\mathcal{R}}]}{\mathcal{F}^{(2)}} = \mathop{\mathbb E}\left[{ \frac{\min\{k', k''\}}{k} }\right] = \frac{1}{k} \sum_{i=1}^{k-1} \min\{ i, k-i \} \begin{pmatrix} k \\ i \end{pmatrix} 2^{-k} \displaystyle \frac{\mathop{\mathbb E}[{\mathcal{R}}]}{\mathcal{F}^{(2)}} = \mathop{\mathbb E}\left[{ \frac{\min\{k', k''\}}{k} }\right] = \frac{1}{k} \sum_{i=1}^{k-1} \min\{ i, k-i \} \begin{pmatrix} k \\ i \end{pmatrix} 2^{-k}](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cfrac%7B%5Cmathop%7B%5Cmathbb+E%7D%5B%7B%5Cmathcal%7BR%7D%7D%5D%7D%7B%5Cmathcal%7BF%7D%5E%7B%282%29%7D%7D+%3D+%5Cmathop%7B%5Cmathbb+E%7D%5Cleft%5B%7B+%5Cfrac%7B%5Cmin%5C%7Bk%27%2C+k%27%27%5C%7D%7D%7Bk%7D+%7D%5Cright%5D+%3D+%5Cfrac%7B1%7D%7Bk%7D+%5Csum_%7Bi%3D1%7D%5E%7Bk-1%7D+%5Cmin%5C%7B+i%2C+k-i+%5C%7D+%5Cbegin%7Bpmatrix%7D+k+%5C%5C+i+%5Cend%7Bpmatrix%7D+2%5E%7B-k%7D&bg=T&fg=000000&s=0)
since:
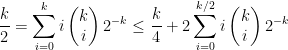
and therefore:
![\displaystyle \frac{\mathop{\mathbb E}[{\mathcal{R}}]}{\mathcal{F}^{(2)}} \geq \frac{1}{4} \displaystyle \frac{\mathop{\mathbb E}[{\mathcal{R}}]}{\mathcal{F}^{(2)}} \geq \frac{1}{4}](http://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cfrac%7B%5Cmathop%7B%5Cmathbb+E%7D%5B%7B%5Cmathcal%7BR%7D%7D%5D%7D%7B%5Cmathcal%7BF%7D%5E%7B%282%29%7D%7D+%5Cgeq+%5Cfrac%7B1%7D%7B4%7D+&bg=T&fg=000000&s=0)

This similar approximations can be extended to more general environments with very little change. For example, for multi-unit auctions, where  we use the benchmark
we use the benchmark 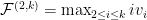 and we can be
and we can be  -competitive against it, by random-sampling, evaluating
-competitive against it, by random-sampling, evaluating  on both sets and running a profit extractor on both. The profit extractor is a simple generalization of the previous one.
on both sets and running a profit extractor on both. The profit extractor is a simple generalization of the previous one.
:
:
as a random variable that indicates the time that a light bulb will take to extinguish. If we are in time
and the light bulb hasn’t extinguished so far, what is the probability it will extinguish in the next
time:
is non-decreasing. This is very natural for light bulbs, for example. Many of the distributions that we are used to are MHR, for example, uniform, exponential and normal. The way that I like to think about MHR distributions is the following: if some distribution has hazard rate
, then it means that
. If we define
, then
, so:
for
. They way I like to think about those distributions is that whenever you are able to prove something about the exponential distribution, then you can prove a similar statement about MHR distributions. Consider those three examples:
for MHR distributions. This fact is straightforward for the exponential distribution. For the exponential distribution
and therefore
, therefore
.
iid where
is MHR and
and
, then
. The proof for the exponential distribution is trivial, and in fact, this is tight for the exponential, the trick is to use the convexity of
. We use that
in the following way:
, we have that
. This way, we get:
, then for
,
. Again, this is tight for exponential distribution. The proof is quite trivial:
is a monotone function. I usually find harder to think about regular distributions than to think about MHR (in fact, I don’t know so many examples that are regular, but not MHR. Here is one, though, called the equal-revenue-distribution. Consider
distributed according to
. The cumulative distribution is given by
. The interesting thing of this distribution is that posted prices get the same revenue regardless of the price. For example, if we post any price
, then a customer with valuations
buys the item if
by price
, getting revenue is
. This can be expressed by the fact that
. I was a bit puzzled by this fact, because of Myerson’s Lemma:
with probability
when he has value
, then the revenue is
.
. For example, suppose we fix some price
and we sell the item if
by price
. Then it seems that Myerson’s Lemma should go through by a derivation like that (for this special case, although the general proof is quite similar):
. We wrote:
, which is quite a natural a distribution over valuations of a good. So, one of the bugs of the the equal-revenue-distribution is that
. A family that is close to this, but doesn’t suffer this bug is:
for
, then
. For
we have
, then we get
.
