Home > theory > Entropy

Entropy

August 27th, 2009 Leave a comment Go to comments

Today was the first day of classes here at Cornell and as usual, I attend to a lot of different classes to try to decide which ones to take. I usually feel like I wanted to take them all, but there is this constant struggle: if I take too many classes I have no time to do research and to read random things that happen to catch my attention at that moment, and if I don’t take many classes I feel like not learning a lot of interesting stuff I wanted to be learning. The solution in the middle of the way is to audit a lot of classes and start dropping them as a start needing more time: what happens usually quickly. This particular fall I decided that I need to build a stronger background in probability – since I am finding a lot of probabilistic stuff in my way and I have nothing more than my undergrad course and things I learned on demand. I attended at least three probability classes with different flavours today and I decided to blog about a simple, yet very impressive result I saw in one of them.

Since I took a class on “Principles of Telecommunications” in my undergrad, I became impressed by Shannon’s Information Theory and the concept of entropy. There was one theorem that I always heard about but never saw the proof. I thought it was a somewhat complicated proof, but it turned out not to be that much.

Consder an alphabet {\Omega} and a probability distribution over it. I want to associate to each {\omega \in \Omega} a string {c(\omega)} of {k(\omega)} {\{0,1\}}-digits to represent each simbol of the alphabet. One way of allowing the code to be decodable is to make them a proper code. A proper code is a code such that given any {\omega_1} and {\omega_2}, {c(\omega_1)} is not a prefix of {c(\omega_2)}. There are several codes like this, but some are more efficient then others. Since the letters have different frequencies, it makes sense to code a frequent letter (say ‘e’ in English) with few bits and a letter that doesn’t appear much, say ‘q’ with more bits. We want to find a proper code to minimize:

\displaystyle \mathop{\mathbb E}[k(\omega)] = \sum_{\omega \in \Omega} k(\omega) p(\omega)

The celebrated theorem by Shannon shows that for any proper code (actually it holds more generally for any decodable code), we have {\mathop{\mathbb E}[k(\omega)] \geq H} where {H} is the entropy of the alphabet, defined as:

\displaystyle H = - \sum_{\omega} p(\omega) \log_2 p(\omega)

even more impressive is that we can achieve something very close to it:

Theorem 1 There is a code such that {\mathop{\mathbb E}[k(\omega)] \leq H + 1}.

With an additional trick we can get {H + \epsilon} for any {\epsilon > 0}. The first part is trickier and I won’t do here (but again, it is not as hard as I thought it would be). For proving that there is a code with average length {\leq H + 1} we use the following lemma:

Lemma 2 There is a proper code for {\Omega} with code-lengths {k(\omega)} if and only if {\sum_\omega 2^{-k(\omega)} \leq 1}

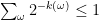
Proof: Let {N = \max_\omega k(\omega)} and imagine all the possible codewords of length {\leq N} as a complete binary tree. Since it is a proper code, no two codes {c(\omega_1)} and {c(\omega_2)} are in the same path to the root. So, picking one node as a codeword means that we can’t pick any node in the subtree from it. Also, for each leave, the is at most one codeword in its path to the root. Therefore we can assign each leaf of the tree to a single codeword or to no codeword at all. It is easy to see that a codeword with size {k(\omega)} has associated with it {2^{N - k(\omega)}} leaves. Since there are {2^N} leaves in total, we have that:

\displaystyle \sum_\omega 2^{N-k(\omega)} \leq 2^N

what proves one direction of the result. Now, to prove the converse direction, we can propose a greedy algorithm: given {\Omega} and {k(\omega)} such that {\sum_\omega 2^{-k(\omega)} \leq 1}, let {N = \max_\omega k(\omega)}. Now, suppose {k(\omega_1) \leq k(\omega_2) \leq k(\omega_3) \leq \hdots}. Start with {2^N} leaves in a whole block. Start dividing them in {2^{k(\omega_1)}} blocks and assign one to {\omega_1}. Now we define the recursive step: when we analyze {\omega_j}, the leaves are divided in {2^{k(\omega_j-1)}} blocks, some occupied, some not. Divide each free block in {2^{k(\omega_j) - k(\omega_j-1)}} blocks and assign one of them to {\omega_j}. It is not hard to see that each block corresponds to one node in the tree (the common ancestor of all the leaves in that block) and that it corresponds to a proper code. \Box

Now, using this we show how to find a code with with {\mathop{\mathbb E}[k(\omega)] \leq H + 1}. For each {\omega}, since {p(\omega) \in (0,1]} we can always find {k(\omega)} such that {\frac{1}{2} p(\omega) \leq 2^{-k(\omega)} \leq p(\omega)}. Now, clearly:

\displaystyle \sum_\omega 2^{-k(\omega)} \leq \sum_\omega p(\omega) = 1

and:

\displaystyle \mathop{\mathbb E}[k(\omega)] = \sum_\omega k(\omega) p(\omega) \leq \sum_\omega [1 - \log_2 p(\omega)] p(\omega) = H + 1

Cool, but now how to bring it to {H + \epsilon} ? The idea is to code multiple blocks at the same time (even if they are independent, we are not taking advantage of correlation between the blocks). Consider {\Omega^k} and the probability function induced on it, i.e.:

\displaystyle p_k (\omega_1, \hdots, \omega_k) = \prod_{i=1}^k p(\omega_i)

It is not hard ot see that {\Omega^k} with {p_k} has entropy {kH} because:

\displaystyle \begin{aligned} \sum_{\omega_1, \hdots, \omega_k} p_k(\omega_1, \hdots, \omega_k) \log_2 p_k(\omega_1, \hdots, \omega_k) =\\ = \sum_{\omega_1, \hdots, \omega_k} \prod_i p(\omega_i) \sum_i \log_2 p(\omega_i) =\\ = \sum_i \sum_\omega p(\omega) \log_2 p(\omega) = kH \end{aligned}

and then we can just apply the last theorem to that: we can find a function that codifies {k} symbols {\omega = (\omega_1, \hdots, \omega_k)} with {l(\omega)} symbols such that:

{kH \leq \mathop{\mathbb E}[l(\omega)] \leq kH + 1} since {l(\omega)} codifies {k} symbols, we are actually interested in {\mathop{\mathbb E}[l(\omega)/k]} and therefore we get:

\displaystyle H \leq \mathop{\mathbb E}\left[\frac{l(\omega)}{k}\right] \leq H + \frac{1}{k}
Categories: theory Tags: , , ,
  1. No comments yet.
  1. No trackbacks yet.